Mathematics - Algebra of continuous functions | 11th Mathematics : UNIT 9 : Differential Calculus Limits and Continuity
Chapter: 11th Mathematics : UNIT 9 : Differential Calculus Limits and Continuity
Algebra of continuous functions
Algebra of continuous functions
If f and g are continuous at x0 then
(1) f + g is continuous at x = x0,
(2) f - g is continuous at x = x0,
(3)f . g is continuous at x = x0, and
(4) f/g is continuous at x = x0 (g(x) ≠ 0).
(5) Composite function theorem on continuity.
If f is continuous at g(x0) and g is continuous at x0 then fog is continuous at x0.
Continuity in a closed interval
Definition 9.9
A function f :[a , b] → R is said to be continuous on the closed interval [a, b] if it is continuous on the open interval (a, b) and
lim x →a f (x ) = f (a) and lim x →b f (x) = f(b).
That is, the function f is continuous from the right at a and continuous from the left at b, and is continuous at each point x0 ∈ (a ,b) .
Illustration 9.7
Discuss the continuity of f(x) = √[1-x2]
The domain of definition of f is the closed interval [-1,1].
(f is defined if 1 - x2 ≥ 0)
For any point c∊ (-1,1)
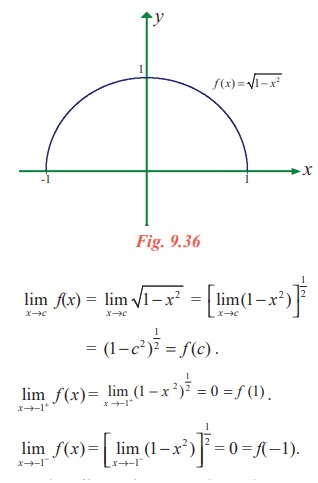
Thus f is continuous on [-1, 1]. One can also solve this problem using composite function theorem.
Example 9.37
Describe the interval(s) on which each function is continuous.
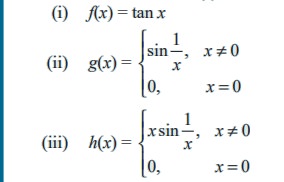
Solution
(i) The tangent function f(x) = tanx is undefined at x = ( 2n +1) π/2, n ∈ Z.
At all other points it is continuous, so f(x) = tan x is continuous on each of the open intervals

Example 9.38
A tomato wholesaler finds that the price of a newly harvested tomatoes is Rs. 0.16 per kg if he purchases fewer than 100 kgs each day. However, if he purchases at least 100 kgs daily, the price drops to Rs. 0.14 per kg. Find the total cost function and discuss the cost when the purchase is 100 kgs.
Solution
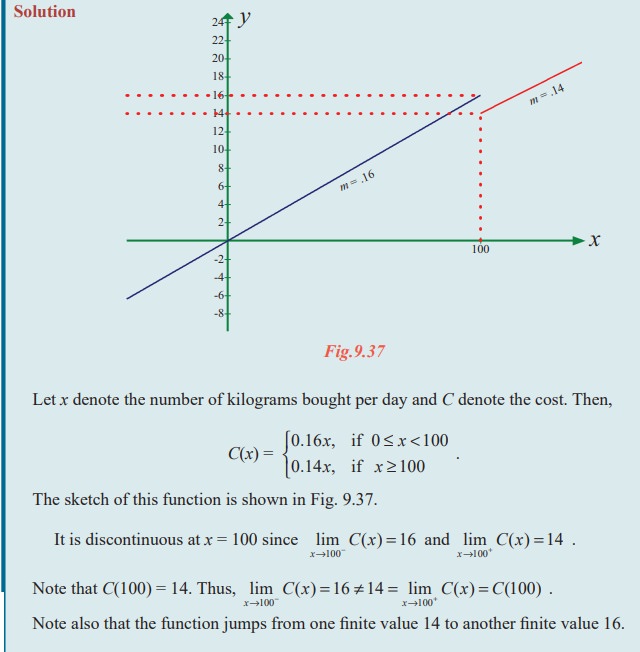
Related Topics