Limits at infinity

Limits at infinity

In the previous section we investigated infinite limits and vertical asymptotes. There, we let x approach a number and the result was that the values of y became arbitrarily large (very large positive or very large negative). In this section, we let x become arbitrarily large (positive or negative) and see what happens to y.

Let’s begin by investigating the behaviour of f : R → R  defined by

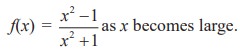
We tabulate the values of this function as in

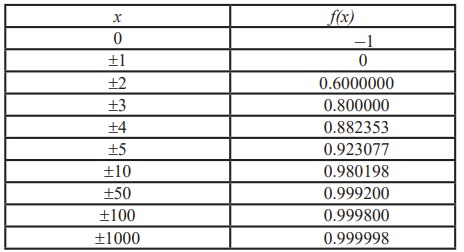
As x grows larger and larger (large positive or large negative) you can see that the values of f(x) gets closer and closer to 1. In fact, it seems that we can make the values of f(x) as close as to 1 by taking x sufficiently large. This situation is expressed symbolically by writing

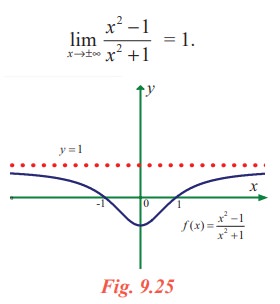
If we look at the graph :

Geometrically, (see Fig. 9.25) this situation also leads us to have

Definition 9.6

The line y = l is called a horizontal asymptote of the curve y = f(x) if either

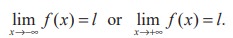
Illustration 9.4

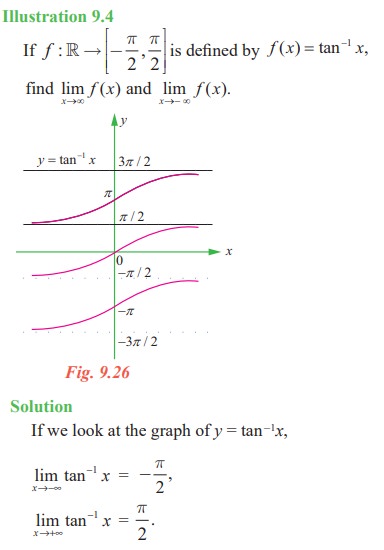
Illustration 9.5

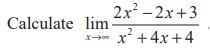
Solution

If we could try to use limit theorems to calculate this limit, we end up in the following situations.

(2x2 – 2x + 3) →∞ as x →∞

( x2 – 4x + 3) →∞ as x →∞

But actual calculation and tabulation gives the following :

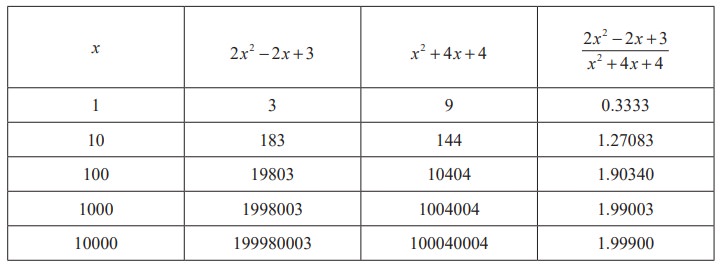
Table values show that as x becomes sufficiently large, f(x) becomes closer and closer to 2. Then,

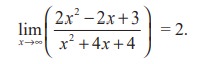
Fortunately, we may simplify the problem by dividing the numerator and denominator by x2. We have

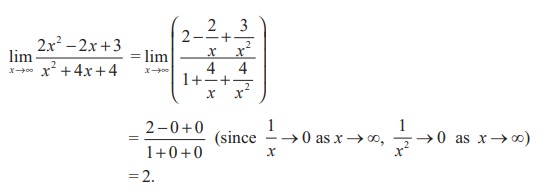
Note that the degree of both numerator and denominator expressions are the same.

In general, the limits as x→±∞ of rational expressions can be found by first dividing the numerator and denominator by the highest power of x that appears in the denominator, and then calculating the limit as x→ ∞ (or x→ - ∞) of both numerator and denominator.