One sided limits: left-hand limit and right-hand limit

One sided limits

Definition 9.2

We say that the left-hand limit of f(x) as x approaches x0 (or the limit of f(x) as x approaches from the left) is equal to l1 if we can make the values of f(x) arbitrarily close to l1 by taking x to be sufficiently close to x0 and less than x0. It is symbolically written as

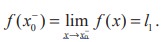
Similarly, we define the right hand limit.

Definition 9.3

We say that the right-hand limit of f(x) as x approaches x0 (or the limit of f(x) as x approaches from the right) is equal to l2 if we can make the values of f(x) arbitrarily close to l2 by taking x to be sufficiently close to x0 and greater than x0. It is symbolically written as

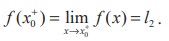
Thus the symbols “ x → x0− ” and “ x → x0+ ” mean that we consider only x < x0 and x > x0 respectively.

These definitions are illustrated in the following Fig. 9.6 to 9.9.

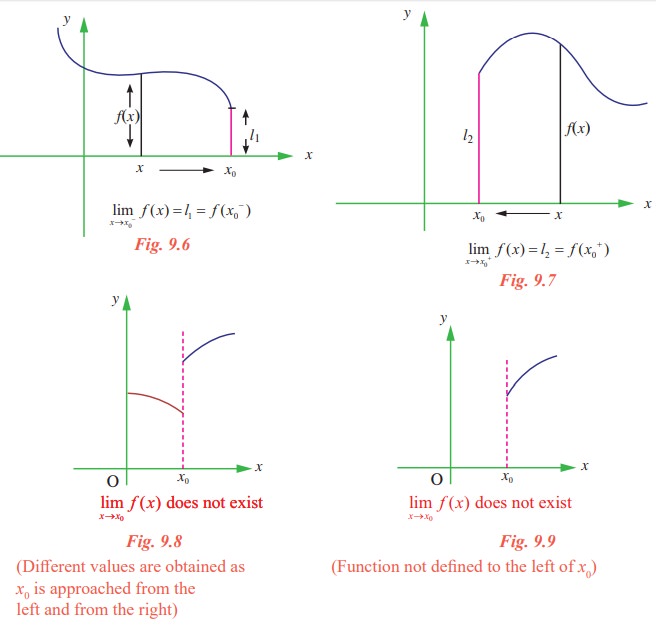
From the above discussions we conclude that 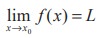exists if the following hold :

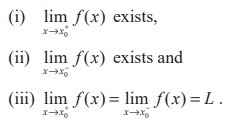
From the definitions of one sided limits and that of the limit of f(x) as we have the following :

Thus, when we say limx →x0 f (x) exists, it is understood that L is a unique real number. If any one of the above conditions fails then we say the limit of f(x) as x approaches x0 does not exist.

We remark that the existence of one sided limits is weaker than the existence of limits.

Sometimes it is very useful to use the following in computing left and right limits. For h > 0,

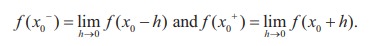
Note that f (x0 -) and f (x0+) stand for the left and right limiting values. But f (x0 ) is the value of the function at x = x 0 .

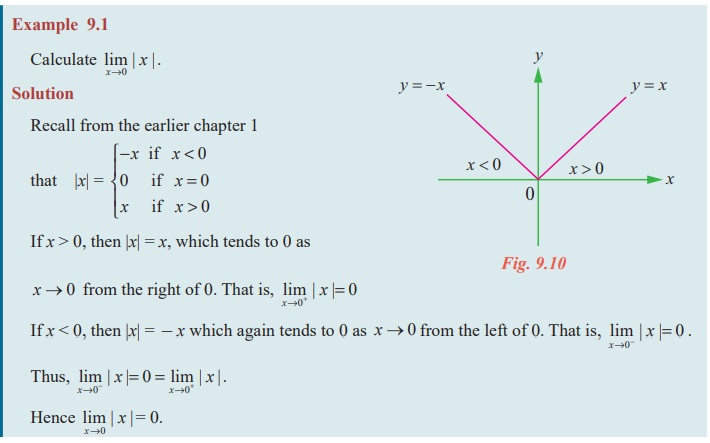
Example 9.1

Calculate lim x→0 | x | .

EXERCISE 9.1

In problems 1-6, complete the table using calculator and use the result to estimate the limit.

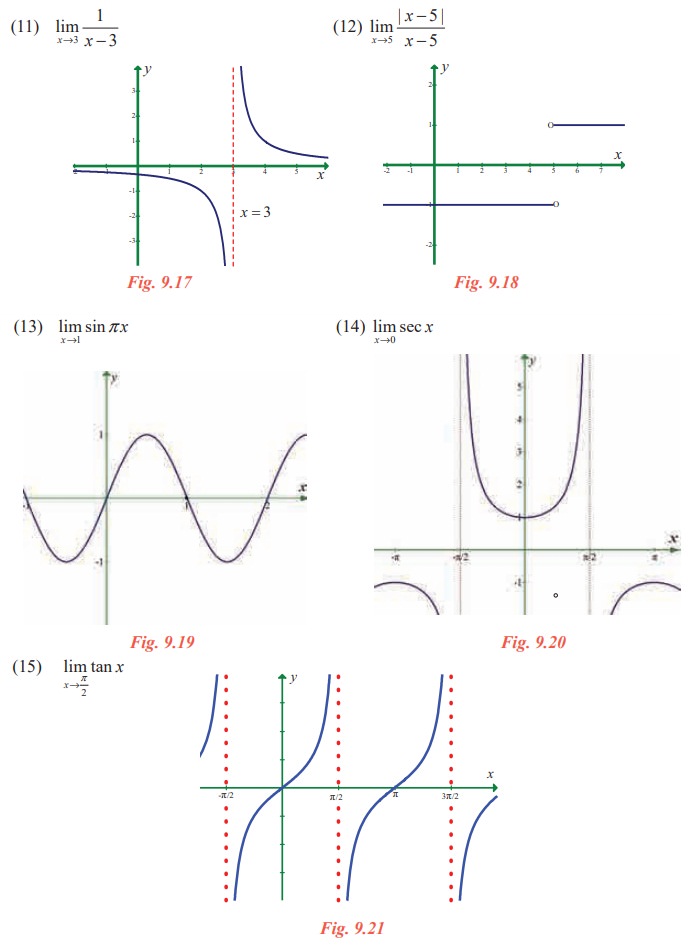
In exercise problems 7 - 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?

Sketch the graph of f, then identify the values of x0 for which lim x →x0 f (x) exists.

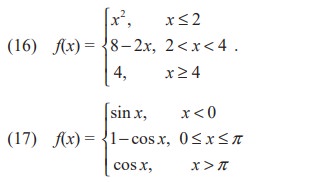
(18) Sketch the graph of a function f that satisfies the given values :

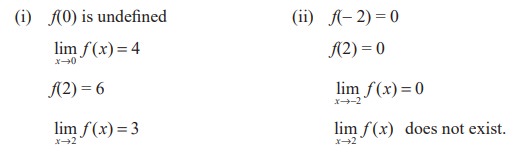
(19) Write a brief description of the meaning of the notation lim x→8f ( x) = 25. .

(20)  If f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2?

(21) If the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning.

(22) Evaluate : 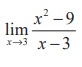if it exists by finding f (3- ) and f (3+) .

(23) Verify the existence of