Differential Calculus - Limits and Continuity | Mathematics - Exercise 9.6: Choose the correct answer | 11th Mathematics : UNIT 9 : Differential Calculus Limits and Continuity
Chapter: 11th Mathematics : UNIT 9 : Differential Calculus Limits and Continuity
Exercise 9.6: Choose the correct answer
Differential Calculus - Limits and Continuity (Mathematics)
Choose the correct or
the most suitable answer from the given four alternatives.
(1) 
(1) 1
(2) 0
(3) ∞
(4) −∞
Ans: (2)
Solution
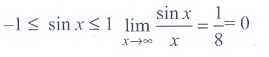
(2) 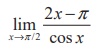
(1) 2
(2) 1
(3) −2
(4) 0
Ans: (3)
Solution
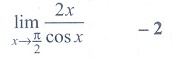
(3) 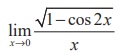
(1) 0
(2) 1
(3) √2
(4) does not exist
Ans: (4)
(4) 
(1) 1
(2) - 1
(3) 0
(4) 2
Ans: (1)
Solution

(5)  is
is
(1) e4
(2) e2
(3) e3
(4) 1
Ans: (1)
(6) 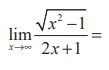
(1) 1
(2) 0
(3) - 1
(4) 1/2
Ans: (4)
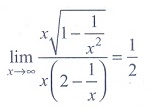
(7) 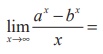
(1) log ab
(2) log (a/b)
(3) log (a/b)
(4) a/b
Ans: (2)
(8) 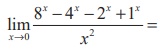
(1) 2 log 2
(2) 2(log 2)2
(3) log 2
(4) 3 log 2
Ans: (2)
(9) If  ,
then the value of limx→0 f (x) is equal to
,
then the value of limx→0 f (x) is equal to
(1) -1
(2) 0
(3) 2
(4) 4
Ans: (2)
(10) 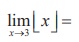
(1) 2
(2) 3
(3) does not exist
(4) 0
Ans: (3)
Solution
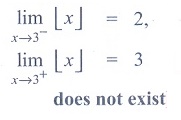
(11) Let the function f
be defined by f (x)= 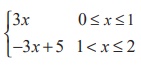 , then
, then

Ans: (4)
Solution
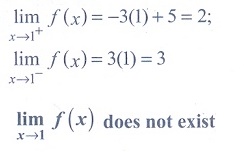
(12) If f : R→
R is defined by 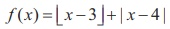 for x ∊ R, then limx→3 f (x) is equal to
for x ∊ R, then limx→3 f (x) is equal to
(1) - 2
(2) - 1
(3) 0
(4) 1
Ans: (3)
(13) 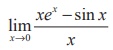 is
is
(1) 1
(2) 2
(3) 3
(4) 0
Ans: (4)
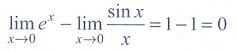
(14) If 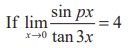 , then the value of p is
, then the value of p is
(1) 6
(2) 9
(3) 12
(4) 4
Ans: (3)
(15)  is
is
(1) √2
(2) 1/√2
(3) 1
(4) 2
Ans: (1)
(16) 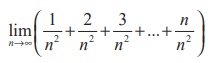 is
is
(1) 1/2
(2) 0
(3) 1
(4) ∞
Ans: (1)
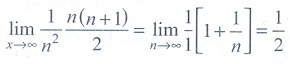
(17) 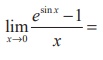
(1) 1
(2) e
(3) 1/ e
(4) 0
Ans: (1)
(18) 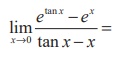
(1) 1
(2) e
(3) 1/ 2
(4) 0
Ans: (1)
(19) The value of 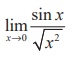 is
is
(1) 1
(2) - 1
(3) 0
(4) ∞
Ans: (4)
(20) The value of 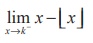 , where k is an integer is
, where k is an integer is
(1) - 1
(2) 1
(3) 0
(4) 2
Ans: (2)
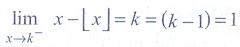
(21) At x = 3/2 the
function f ( x) = | 2x -3 | / 2x -3 is
(1) continuous
(2) discontinuous
(3) differentiable
(4) non-zero
Ans: (2)
Solution
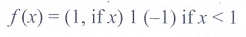
(22) Let f : R→R be
defined by 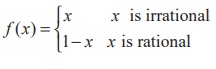 then f is
then f is
(1) discontinuous
at x = 1/2
(2) continuous at x =
1/2
(3) continuous
everywhere
(4) discontinuous
everywhere
Ans: (2)
(23) The function  is not defined for x = −1 . The value of f (−1) so that the
function extended by this value is continuous is
is not defined for x = −1 . The value of f (−1) so that the
function extended by this value is continuous is
(1) 2/3
(2) −2/3
(3) 1
(4) 0
Ans: (2)
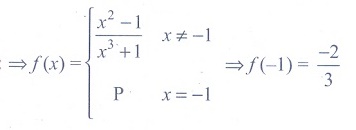
(24) Let f be a
continuous function on [2, 5]. If f takes only rational values for all x
and f (3) = 12, then f(4.5) is equal to
(1) [f (3) + f
(4.5)] / 7.5
(2) 12
(3) 17.5
(4) [f (4.5) − f
(3)] / 1.5
Ans: (2)
Solution
f is a constant function
(25) Let a
function f be defined by f (x) = x−|x| / x for x ≠ 0
and f (0) = 2 . Then f is x
(1) continuous
nowhere
(2) continuous
everywhere
(3) continuous for all x
except x = 1
(4) continuous for all x
except x = 0
Ans: (4)
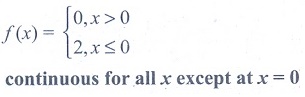
Related Topics