Infinite Limits

Infinite limits

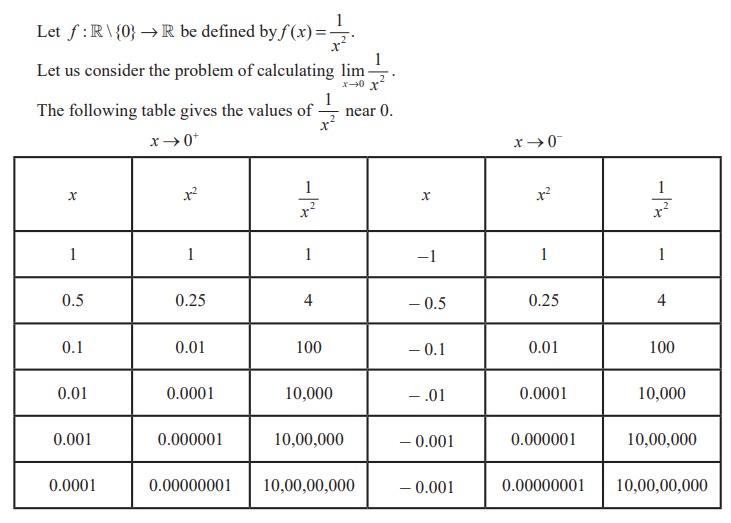
The table values tell us that as x gets closer and closer to 0, f(x) = 1/ x2 gets larger and larger. In fact, 1/x2 grows without bound as x approaches 0 from either side. In this situation we say that f(x) tends to infinity as x approaches zero and write 1/x2 → ∞ as x → 0− and 1/x2 → ∞ as x → 0+ and hence 1/x2 → ∞ as x → 0 .

Geometrically, x = 0 namely the y-axis is a vertical asymptote to the curve representing f(x) = 1/x2 .

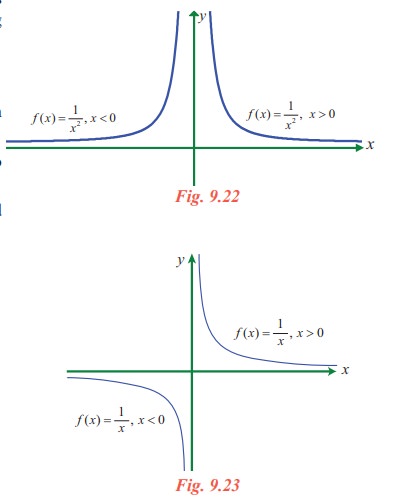
The graph of the function f(x) = 1/x2 is shown in Fig. 9.22.

Remember that the limit is infinite and so  lim x→0 1/x2 does not exist. Students are cautioned that ∞ is a symbol for this behaviour of f(x) = 1/x2 and is not a new number.

Similarly, if we look at f(x) = 1/x,  it is easy to see that, 1/x → −∞ as x → 0−  and 1/x → +∞ as x → 0+  which is geometrically clear from the graph of  f(x) = 1/x (Fig. 9.23) .

In general we have the following intuitive  definitions.

Definition 9.4

For a given M > 0, open intervals of the form (M, ∞) is called neighbourhood of ∞.

Similarly, for given K < 0, open intervals of the form (-∞, K) is called neighbourhood of - ∞.

Definition 9.5

We say,  f ( x) → ∞ as x approaches x0 if for given positive number M there is a neighbourhood of x0, such that whenever x is in the neighbourhood of x0 , f ( x )> M . i.e., f ( x) ∊ (M , ∞ ).

Similarly, f ( x) → - ∞ as x approaches x0 if for a given K < 0 there is a neighbourhood of x0 such that whenever x is in the neighbourhood of x0 , f ( x ) < K.  i.e.,  f ( x) ∊  (- ∞, K ).

To describe this situation symbolically, we write

f (x ) → ∞ as x → x0

f (x ) → −∞ as x → x0

f (x ) → ∞ as x → x0−

f (x ) → −∞ as x → x0+

and f (x ) → ∞ as x → x0+

f (x ) → −∞ as x → x0−

are called infinite limits. If any one of the foregoing conditions hold, then the line x = x0 is a vertical asymptote for the graph of f(x).

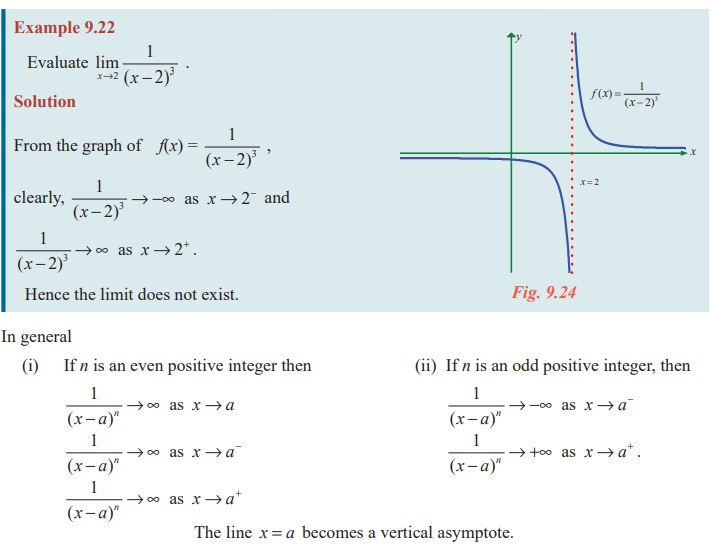
Example 9.21

Solution

One can tabulate values of x near 0 (from either side) and conclude f (x) = 1/[x2+x3] grows without bound and hence f (x ) → ∞ as x → 0 .

To calculate this limit without making a table, we first divide the numerator and denominator by x2. This division can be done, since in the calculation of the limit x ≠ 0 and hence x2 ≠ 0. We can have

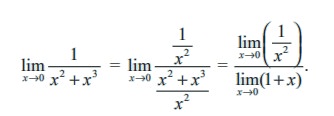
Thus the numerator grows without bound while the denominator approaches 1, implying that 1/(x2 + x3) does tend to infinity.

This example illustrates how a difficult calculation can be greatly simplified by a few algebraic manipulations.