Limits of rational functions

Limits of rational functions

If R (x) = p(x)/ q (x) and the degree of the polynomial p(x) is greater than the degree of q(x), then

If the degree of q(x) is greater than the degree of p(x), then

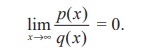
Finally, if the degree of p(x) is equal to the degree of q(x), then

Remark

We reemphasize that statements such as f (x ) → ∞ as x → a , f (x ) → −∞ as x → a, and f (x ) → ∞ as x → ∞ , f (x ) → −∞ as x → ∞ mean that the limits do not exist. The symbol ∞ does not represent a number and should not be treated as a number.