Applications of limits

Applications of limits

Example 9.25

Alcohol is removed from the body by the lungs, the kidneys, and by chemical processes in liver. At moderate concentration levels, the majority work of removing the alcohol is done by the liver; less than 5% of the alcohol is eliminated by the lungs and kidneys. The rate r at which the liver processes alcohol from the bloodstream is related to the blood alcohol concentration x by a rational function of the form r(x) = αx / [ x + β] for some positive constants a and b. Find the maximum possible rate of removal.

Solution

As the alcohol concentration x increases the rate of removal increases.

Therefore, the maximum possible rate of removal =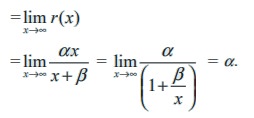

Example 9.26

According to Einstein’s theory of relativity, the mass m of a body moving with velocity v is 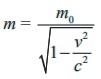, where m0 is the initial mass and c is the speed of light. What happens to m as v → c-. Why is a left hand limit necessary?

Solution

That is, the mass becomes very very large (infinite) as v → c−.

The left hand limit is necessary. Otherwise as ν → c+ makes 1− v2/c2 < 0 and consequently we cannot find the mass.

Example 9.28

Suppose that the diameter of an animal’s pupils is given by 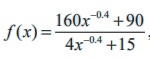, where x is the intensity of light and f(x) is in mm. Find the diameter of the pupils with (a) minimum light (b) maximum light.

Solution

(a)  For minimum light it is enough to find the limit of the function when x → 0+.

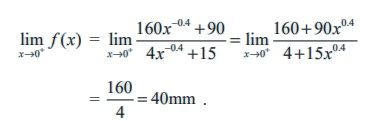
(b) For maximum light, it is enough to find the limit of the function when x → ∞

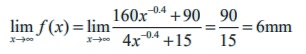
That is, the pupils have a limiting size of 6mm, as the intensity of light is very large.

EXERCISE 9.3

(9) An important problem in fishery science is to estimate the number of fish presently spawning in streams and use this information to predict the number of mature fish or “recruits” that will return to the rivers during the reproductive period. If S is the number of spawners and R the  number of recruits, “Beverton-Holt spawner recruit function” is R(S) = S / (α S + β ) where α and β are positive constants. Show that this function predicts approximately constant recruitment when the number of spawners is sufficiently large.

(10) A tank contains 5000 litres of pure water. Brine (very salty water) that contains 30 grams of salt per litre of water is pumped into the tank at a rate of 25 litres per minute. The concentration of salt water after t minutes (in grams per litre) is C(t) = 30t / 200+t

What happens to the concentration as t →∞?