Chapter: 11th Chemistry : UNIT 2 : Quantum Mechanical Model of Atom
Solved Example Problems: Chemistry: Quantum Mechanical Model of Atom
Quantum Mechanical Model of Atom | Chemistry
Solved Example Problems
27. How many orbitals are possible for n =4?
Answer:
n = 4 l = 0, 1, 2, 3
four sub-shells ⇒ s, p, d, f
l = 0ml = 0 ; one 4s orbital.
l = 1 ml = –1, 0, +1 ; three 4p orbitals.
l = 2 ml = –2, –1, 0, +1, +2 ; five 4d orbitals.
l = 3 ml = -3, –2, –1, 0, +1, +2 , +3; seven 4f orbitals
Over all Sixteen orbitals.
4s, 4p, 4d and 4f orbitals = 1 + 3 + 5 + 7
= 16 Orbitals
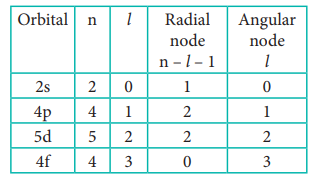
28. How many radial nodes for 2s, 4p, 5d and 4f orbitals exhibit? How many angular nodes?
Answer:
29. The stabilisation of a half filled d - orbital is more pronounced than that of the p-orbital why?
"More exchange energy, increases the stability of orbitals"
Over all electron exchange for d - Orbitals = 10
Over all electron exchange for p - Orbitals = 6
Hence, Half filled d - orbitals are more stable.
30. Consider the following electronic arrangements for the d5 configuration.
(i) which of these represents the ground state
(ii) which configuration has the maximum exchange energy.
Answer:
i) (c) represents the ground state among the given three d5 electronic arrangements.
ii) Also, (c) has the maximum exchange energy.
31. State and explain pauli's exclusion principle.
No two electrons in an atom can have the same set of values of four quantum numbers.
32. Define orbital? what are the n and l values for 3px and 4dx2-y2 electron?
Answer:
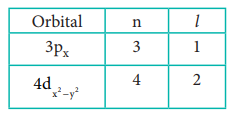
Orbital is a three dismerisional space in which the probability of finding the electron is maximum
33. Explain briefly the time independent schrodinger wave equation?
Based on the Heisenberg's principle and the dual nature of the microscopic particles, Schrodinger expressed the wave nature of electron in terms of a differential equation.
This equation determines the change of wave function in space depending on the field of force in which the electron moves.
This equation does not contain time (t) as a variable and is reffered to as time independent Schordinger wave equation.
34. Calculate the uncertainty in position of an electron, if Δv = 0.1% and υ = 2.2 x106 ms-1
Answer:
Given: Δ = 0.1%
V = 2.2 × 106 ms−1.
ΔV = [0.1 / 100] × 2.2 × 106 ms−1= 2.2 × 103 ms−1
Solution:
Δx.m.Δv ≥ h/4π
Δ × 9.1×10−31Kg × 2.2 × 103 ms−1 ≥ [(6.626 × 10 −34 ) / 4π ] Kgm2 s−1
Δx ≥ ( 6.626 × 10−34 Kgm2 s−1 ) / (9.1×10−31Kg × 2.2 × 103 ms1 × 4π)
≥ ( 6.626 × 10−34 ) / ( 251.45 × 10−28 ) = 0.02635 × 10-6
Δx ≥ 2.635 × 10-8 m
[Alternative Answer]
35. Determine the values of all the four quantum numbers of the 8th electron in O- atom and 15th electron in Cl atom and the last electron in chromium
Answer:
The 8th electron of O - atom is present in 2Px orbital
The 15th electron of Cl atom is present in 3Pz orbital
[Alternative Answer]
36. The quantum mechanical treatment of the hydrogen atom gives the energy value:
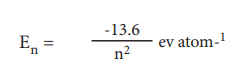
i) use this expression to find ΔE between n = 3 and m=4
ii) Calculate the wavelength corresponding to the above transition.
Answer:
(i) E3 = − 13.6 / 32 = −1.51 eV atom−1
En = − 13.6 / n² = eV atom−1
E4 = − 13.6 / 4² = −0.85 eV atom−1
ΔE = (E4 – E3) = (− 0.85) – (−1.51) = 0.66 eV atom−1
(ii) Energy difference ΔE = 0.66 eVatom−1
= 0.66 × 1.6 × 10−l9J
= 1.06 × 10−19J
= hγ
h (c/λ) = 1.06 ×10−19 J
λ = (hc) / (1.06 × 10−19) J
= (6.626 × 10−34JS × 3× 108ms−1 ) / ( 1.06 × 10−19 ) J
λ = 1.875× l0−6 m
37. How fast must a 54g tennis ball travel in order to have a de Broglie wavelength that is equal to that of a photon of green light 5400Ã…?
Answer:
λ = 5400A0 = 5400 × 10−10 m ; m = 54g
λ = 54 × 10−3 Kg ;
V = ?
λ = h / mV ;
V = h/mλ
= [ 6.626 ×10−34 Kgm2s−1 ] / [ 54× 10−3 Kg × 5400 × 10−10 m]
V = 2.27 × 10−26 ms−1
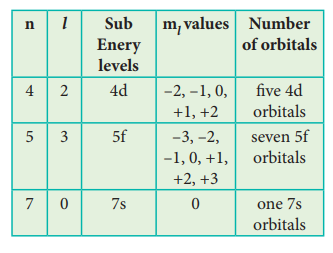
38. For each of the following, give the sub level designation, the allowable m values and the number of orbitals
i) n = 4, l =2, ii) n =5, l = 3 iii) n=7, l=0
Answer:
39. Give the electronic configuration of Mn2+ and Cr3+
Electronic configuration of Mn2+ and Cr3+
25Mn2+ (23 e−S): 1s22s2 2p6 3s23p64s03d5
24Cr3+ (21 e−S): ls22s22p63s23p64s03d3
40. Describe the Aufbau principle
In the ground state of the atoms, the orbitals are filled in the order of their increasing energies.
That is once the lower energy orbitals are completely filled that the electrons enter the next higher energy orbitals.
41. An atom of an element contains 35 electrons and 45 neutrons. Deduce
i) the number of protons
ii) the electronic configuration for the element
iii) All the four quantum numbers for the last electron
Answer:
An atom of an element contains 35 electrons and 45 neutrons having
1) The number of protons = 35
ii) The electronic configuration
= 1s2 2s2 2p6 3s2 3p6 4s2 3d104p5
iii) Four quantum numbers of the last electron
(4p5)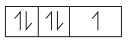 
n = 4; l = 1; m = 0; s = −1/2
[Alternative Answer]
42. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wave length associated with the electron revolving arround the nucleus.
To Prove
"The Circumference of the circular orbit is an integral multiple of wave length"
That is,
Circumference 2πr = nλ
If n = 5, 2πr = 5λ
43. Calculate the energy required for the process.
He+ (g) → He2+ (g) + e-
The ionisation energy for the H atom in its ground state is - 13.6 ev atom-1.
Answer:
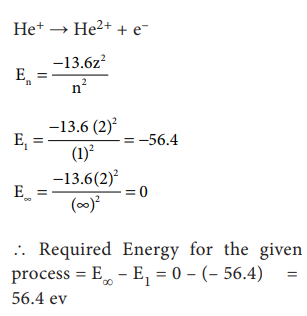
[Alternative Answer]
He+(g) → He2+(g) + e− E= ?
(Ionisation energy of H is = 13.6 eVatom−1)
En = −13.6Z2 / n2
E1 = [−13.6 / 12 ] × (2)2 = −56.4ev
(∴Atomic number of He = 2)
Eα = [−13.6 × (2)2 ] / ∞2 = 0 ev
The required energy of the process = E∞ − E1
= 0 − (−56.4)
= 56.4 eV
44. An ion with mass number 37 possesses unit negative charge. If the ion contains 11.1% more neutrons than electrons. Find the symbol of the ion.
Answer:
Let the mono negative ion with mass number 37 be 37z x−
No of protons + No of neutrons = 37
Let the no of electrons = x
∴ The no of protons = x−1
no of neutrons = 11. % of the no of electrons
= x + 11.1 % x
= x + [11.1 / 100]x
= 11.1 x
=> (x−1) + 11.1 x = 37
2.11x − 1 = 37 => 2.11x = 38 => x = 38 / 2.11 = 18
∴ Atomic number Z = No .of Protons =
= x − 1 = 17
Hence, The given ion is 3717Cl−
[Alternative Answer]
45. The Li2+ ion is a hydrogen like ion that can be described by the Bohr model. Calculate the Bohr radius of the third orbit and calculate the energy of an electron in 4th orbit.
Answer:
Bohr’s radius γn = [ 0.529n2 / Z ] A0
Energy of electron En = [ −13.6z2/ n2 ] eV atom−1
For Li2+ Atomic number = 3,
and number of electrons = 1
i) Bohr radius for the 3rd orbit
r3 = 0529(3)2 / 3 = l.587 A0
ii) Energy of an electron in the 4th Orbit
E4 = (−13.6(3)2 ) / 42 = −7.65 eV atom−1
46. Protons can be accelerated in particle accelerators. Calculate the wavelength (in Å) of such accelerated proton moving at 2.85 ×108 ms-1 ( the mass of proton is 1.673 × 10-27 Kg).
Answer:
V= 2.85 × l08 ms−1
mp= 1.673 × 10−27 kg
λ = ?
λ = h / mv
= [ 6.626 × 10−34Kg m2s−1 ] / [1.673 × 10−27Kg × 2.85 × 108ms−1 ]
= [ ( 6.626 ) / ( 1.673× 2.8 ) ]× 10−15 m
λ = 1.389 × 10−15m (or) 1.389 × 10-5 A0
47. What is the de Broglie wavelength (in cm) of a 160g cricket ball travelling at140 Km hr-1.
Answer:
V = 140 kmhr−1 = [(140 × 1000) / 3600] ms−1 = 38.88ms−1
m = 160 g = 160 × l0−3 Kg;
Solution : λ = h / mv
= [6.626 × 10−34Kgm2s−1 ] / [ 160 × 10−3Kg × 38.88ms−1]
= [(6.626) / (160 × 38.88)] × 10−31m
= 1.065× 10−34 m
λ = 1.065× 10−32cm
48. Suppose that the uncertainty in determining the position of an electron in an orbit is 0.6 Ã…. What is the uncertainty in its momentum?
Answer:
Δx = 0.6A0 ;
Δ p = ?
Δx Δp ≥ h / 4π
0.6 × 10−10m × Δ p ≥ (6.626 × 10−34 ) / 4π
Δp ≥ [ ( 6.626 × 10−34 ) / ( 0.6 × 10−10 × 4π) ] Kgm2s−1
Δp ≥ 0.879 × 10−24 Kgms−1
49. Show that if the measurement of the uncertainty in the location of the particle is equal to its de Broglie wavelength, the minimum uncertainty in its velocity is equal to its velocity / 4Ï€
Answer:
If, Δx = λ Then V = ?
Δx Δp ≥ h / 4π
λ m ΔV ≥ h/4π
⇒ ΔV ≥ h / 4π(mλ)
⇒ ΔV ≥ h / [4πm(h/mv)]
(as λ=h/mv)
⇒ ΔV ≥ V / 4π (Proved)
[Alternative Answer]
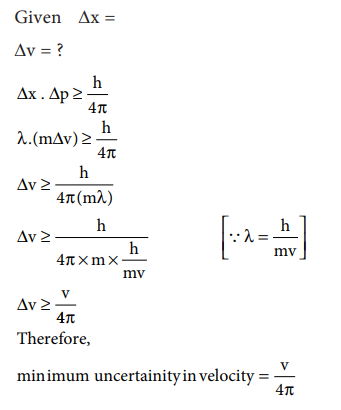
50. What is the de Broglie wave length of an electron, which is accelerated from the rest, through a potential difference of 100V?
Answer:
Potential difference = 100V
= 100 × l.6 × l0−19 J = 1.6 × 10−17J
λ = ?
λ= h / √(2meV)
= [ 6.26 × 10−34 Kgm2s−1 ] / √[ 2×9.1×10−31Kg × 1.6×10−17J ]
= [ 6.26 × 10−34] / √[ 29.12×10−48]
= [ 6.26 × 10−34] / [ 5.4×10−24]
λ = 1.227 × 10−10 m (or) 1.227A0
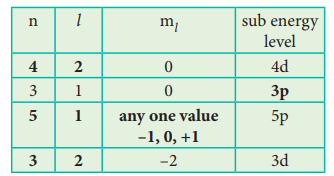
51. Identify the missing quantum numbers and the sub energy level
Answer:
Related Topics