Chapter: 11th Chemistry : UNIT 2 : Quantum Mechanical Model of Atom
Quantum numbers
Quantum
numbers
The electron in an atom can be characterised by a set of
four quantum numbers, namely principal quantum number (n), azimuthal quantum
number (l), magnetic quantum number (m) and spin quantum number (s). When
Schr├Čdinger equation is solved for a wave function ╬©, the solution contains the
first three quantum numbers n, l and m. The fourth quantum number arises due to
the spinning of the electron about its own axis. However, classical pictures of
species spinning around themselves are incorrect.
Principal quantum number (n):
This quantum number represents the energy level in which
electron revolves around the nucleus and is denoted by the symbol 'n'.
1. The 'n' can have the values 1, 2, 3,ŌĆ” n=1 represents K
shell; n=2 represents L shell and n = 3, 4, 5 represent the M, N, O shells,
respectively.
2. The maximum number of electrons that can be
accommodated in a given shell is 2n2.
3. 'n' gives the energy of the electron, En=
(-1312.8)Z2/n2 kJ mol-1 1 and the distance of
the electron from the nucleus is given by rn=(0.529)n2/Z
A
Azimuthal Quantum number (l) or subsidiary quantum number :
1. It is represented by the letter 'l', and can take integral values from zero to n-1, where n is the
principal quantum number
2. Each l value
represents a subshell (orbital). l = 0, 1, 2, 3 and 4 represents the s, p, d, f
and g orbitals respectively.
3. The maximum number of electrons that can be
accommodated in a given subshell (orbital) is 2(2l+1).
4. It is used to calculate the orbital angular momentum
using the expression
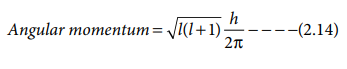
Magnetic quantum number (ml):
1. It is denoted by the letter 'ml'. It takes
integral values ranging from -l to +l through 0. i.e. if l=1; m = -1, 0 and +1
2. Different values of m for a given l value, represent
different orientation of orbitals in space.
3. The Zeeman Effect (the splitting of spectral lines in a
magnetic field) provides the experimental justification for this quantum
number.
4. The magnitude of the angular momentum is determined by
the quantum number l while its
direction is given by magnetic quantum number.
Spin quantum number (ms):
1. The spin quantum number represents the spin of the
electron and is denoted by the letter 'ms'
2. The electron in an atom revolves not only around the
nucleus but also spins. It is usual to write this as electron spins about its
own axis either in a clockwise direction or in anti-clockwise direction. The
visualisation is not true. However spin is to be understood as representing a
property that revealed itself in magnetic fields.
3. Corresponding to the clockwise and anti-clockwise
spinning of the electron, maximum two values are possible for this quantum
number.
4. The values of 'ms' is equal to -┬Į and +┬Į
Table 2.1 Quantum numbers and its significance
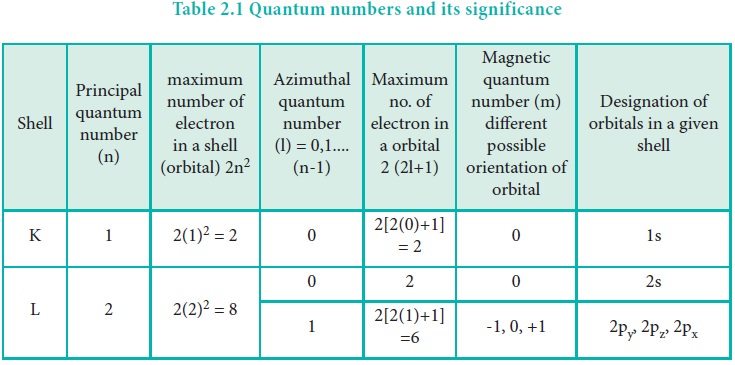
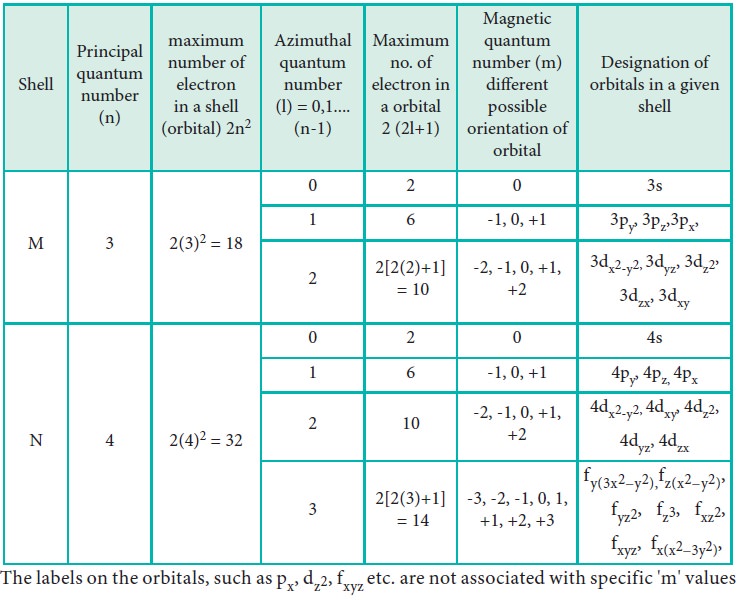
The labels on the orbitals, such as px, dz2,
fxyz etc. are not associated with specific 'm' values
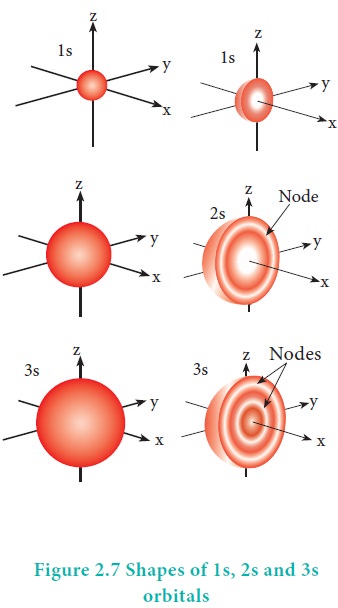
Shapes of atomic orbitals:
The solution to SchrÛdinger equation gives the permitted
energy values called eigen values and the wave functions corresponding to the
eigen values are called atomic orbitals. The solution (╬©) of the Schr├¢dinger
wave equation for one electron system like hydrogen can be represented in the
following form in spherical polar coordinates r, ╬Ė, Žå as,
╬© (r, ╬Ė, Žå) = R(r).f(╬Ė).g(Žå) ------ (2.15)
(where R(r) is called radial wave function, other two
functions are called angular wave functions)
As we know, the ╬© itself has no physical meaning and the
square of the wave function |╬©|2 is related to the probability of
finding the electrons within a given volume of space. Let us analyse how |╬©|2
varies with the distance from nucleus (radial distribution of the probability)
and the direction from the nucleus (angular distribution of the probability).
Radial distribution function:
Consider a single electron of hydrogen atom in the ground
state for which the quantum numbers are n=1 and l=0. i.e. it occupies 1s
orbital. The plot of R(r)2 versus r for 1s orbital is given in Figure
2.3
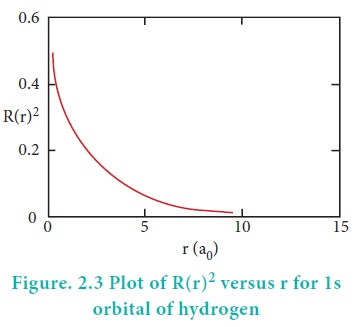
The graph shows that as the distance between the electron
and the nucleus decreases, the probability of finding the electron increases.
At r=0, the quantity R(r)2 is maximum i.e. The maximum value for |╬©|2
is at the nucleus. However, probability of finding the electron in a given
spherical shell around the nucleus is important. Let us consider the volume
(dV) bounded by two spheres of radii r and r+dr.

The plot of 4ŽĆr2╬©2 versus r is given
below.
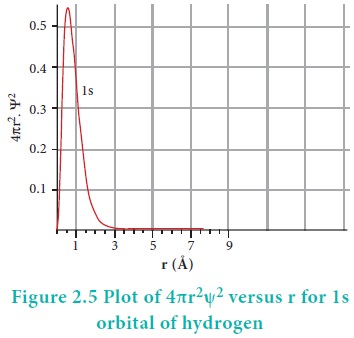
The above plot shows that the maximum probability occurs
at distance of 0.52 ├ģ from the
nucleus. This is equal to the Bohr radius. It indicates that the maximum
probability of finding the electron around the nucleus is at this distance.
However, there is a probability to find the electron at other distances also.
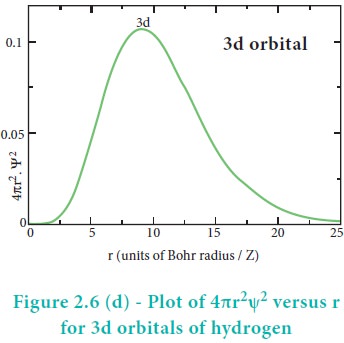
The radial distribution function of 2s, 3s, 3p and 3d orbitals of the hydrogen
atom are represented as follows.
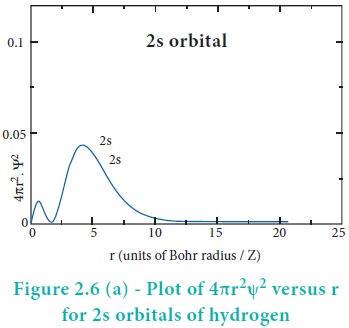
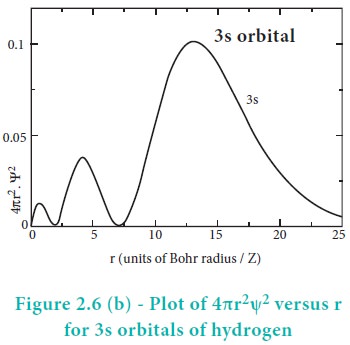
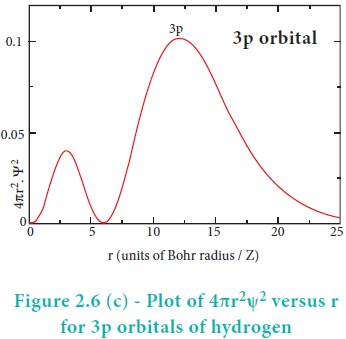
For 2s orbital, as the distance from nucleus r increases,
the probability density first increases, reaches a small maximum followed by a
sharp decrease to zero and then increases to another maximum, after that
decreases to zero. The region where this probability density function reduces
to zero is called nodal surface or a radial node. In general, it has been found
that ns-orbital has (nŌĆō1) nodes. In other words, number of radial nodes for 2s
orbital is one, for 3s orbital it is two and so on. The plot of 4ŽĆr2Žł2
versus r for 3p and 3d orbitals shows similar pattern but the number of radial
nodes are equal to(n-l-1) (where n is
principal quantum number and l is azimuthal quantum number of the orbital).
Angular distribution function:
The variation of the probability of locating the electron
on a sphere with nucleus at its centre depends on the azimuthal quantum number
of the orbital in which the electron is present. For 1s orbital, l=0 and m=0.
f(╬Ė) = 1/ŌłÜ2 and g(Žå) = 1/ŌłÜ2ŽĆ. Therefore, the angular distribution function is
equal to 1/2ŌłÜŽĆ. i.e. it is independent of the angle ╬Ė and Hence, the
probability of finding the electron is independent of the direction from the
nucleus. The shape of the s orbital is spherical as shown in the figure 2.7
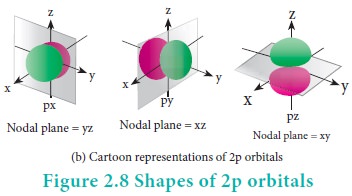
For p orbitals l=1
and the corresponding m values are -1, 0 and +1. The angular distribution
functions are quite complex and are not discussed here. The shape of the p
orbital is shown in Figure 2.8. The three different m values indicates that
there are three different orientations possible for p orbitals. These orbitals
are designated as px, py and pz and the
angular distribution for these orbitals shows that the lobes are along the x, y
and z axis respectively. As seen in the Figure 2.8 the 2p orbitals have one
nodal plane.
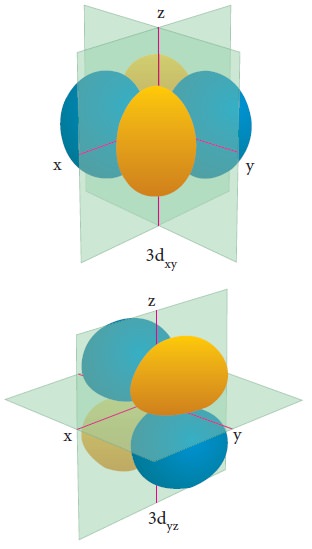
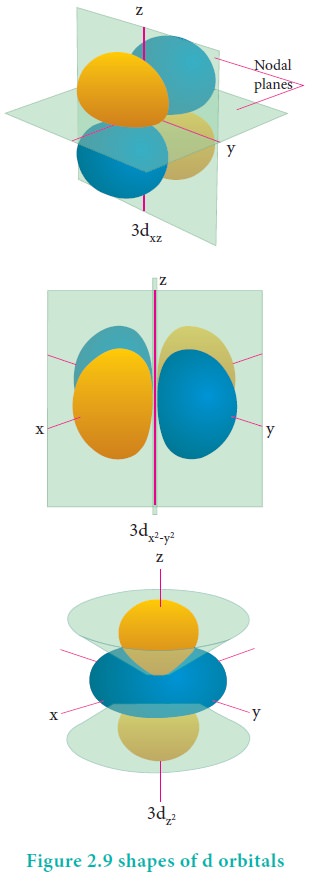
For ŌĆśdŌĆÖ
orbital l = 2 and
the corresponding m values are -2, -1, 0 +1,+2. The shape of the d
orbital looks like a 'clover leaf '. The five m values give rise to five d
orbitals namely dxy , dyz, dzx, dx2,
dz2, and dz2. The 3d orbitals contain two nodal planes as
shown in Figure 2.9.
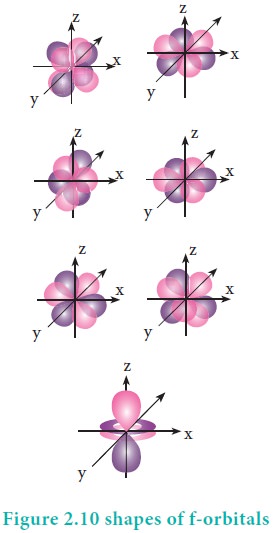
For 'f ' orbital, l
= 3 and the m values are -3, -2,-1, 0, +1, +2, +3 corresponding to seven f
orbitals fz3, fxz2, fyz2, fxyz, fz(x2ŌłÆy2),
fx(x2ŌłÆ3y2), fy(3x2ŌłÆy2),
which are shown in Figure 2.10. There are 3 nodal planes in the
f-orbitals.
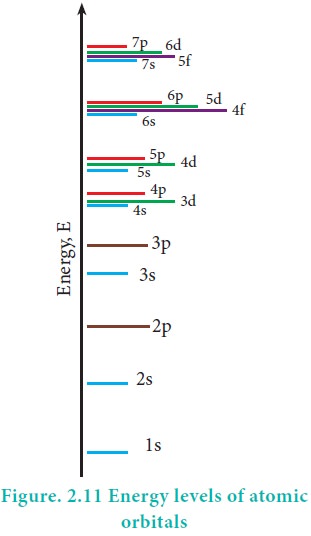
Energies of orbitals
In hydrogen atom, only one electron is present. For such
one electron system, the energy of the electron in the nth orbit is
given by the expression
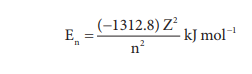
From this equation, we know that the energy depends only
on the value of principal quantum number. As the n value increases the energy
of the orbital also increases. The energies of various orbitals will be in the
following order:
1s < 2s = 2p < 3s = 3p = 3d <4s = 4p = 4d = 4f
< 5s = 5p = 5d = 5f < 6s = 6p = 6d = 6f < 7s
The electron in the hydrogen atom occupies the 1s orbital
that has the lowest energy. This state is called ground state. When this
electron gains some energy, it moves to the higher energy orbitals such as 2s,
2p etcŌĆ” These states are called excited states.
However, the above order is not true for atoms other than
hydrogen (multi-electron systems). For such systems the Schr├Čdinger equation is
quite complex. For these systems the relative order of energies of various
orbitals is given approximately by the (n+l) rule. It states that, the lower
the value of (n + l) for an orbital, the lower is its energy. If two orbitals
have the same value of (n + l), the orbital with lower value of n will have the
lower energy. Using this rule the order of energies of various orbitals can be
expressed as follows.
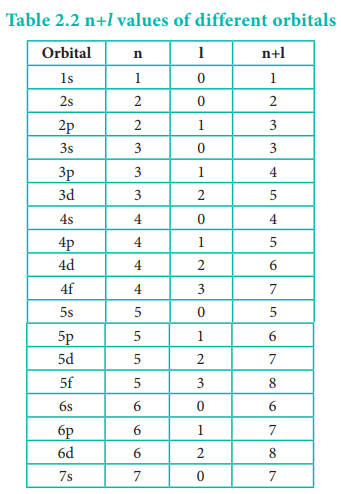
Based on the (n+l) rule, the increasing order of energies
of orbitals is as follows:
1s < 2s < 2p < 3s < 3p < 4s <3d <4p
<5s<4d < 5p < 6s<4f< 5d < 6p < 7s < 5f < 6d
As we know there are three different orientations in space
that are possible for a p orbital. All the three p orbitals, namely, px,
py and pz have same energies and are called degenerate
orbitals. However, in the presence of magnetic or electric field the degeneracy
is lost.
In a multi-electron atom, in addition to the electrostatic
attractive force between the electron and nucleus, there exists a repulsive
force among the electrons. These two forces are operating in the opposite
direction. This results in the decrease in the nuclear force of attraction on
electron. The net charge experienced by the electron is called effective
nuclear charge. The effective nuclear charge depends on the shape of the
orbitals and it decreases with increase in azimuthal quantum number l. The order of the effective nuclear
charge felt by a electron in an orbital within the given shell is s > p >
d > f. Greater the effective nuclear charge, greater is the stability of the
orbital. Hence, within a given energy level, the energy of the orbitals are in
the following order. s < p < d < f.
The energies of same orbital decrease with an increase in
the atomic number. For example, the energy of the 2s orbital of hydrogen atom
is greater than that of 2s orbital of lithium and that of lithium is greater
than that of sodium and so on, that is, E2s(H) > E2s(Li)
> E2s(Na) > E2s(K).
Related Topics