Chapter: 11th Chemistry : UNIT 2 : Quantum Mechanical Model of Atom
Brief questions and answers: Chemistry: Quantum Mechanical Model of Atom
Quantum Mechanical Model of Atom | Chemistry
Answer the following questions
26. Which quantum number reveal information about the shape, energy, orientation and size of orbitals?
i)
Principal quantum number (n)
ii)
Azimuthal quantum number (l)
iii)
Magnetic quantum number (m1)
27. How many orbitals are possible for n =4?
Answer:
n = 4 l = 0, 1, 2, 3
four sub-shells ŌćÆ s, p, d, f
l = 0ml = 0 ; one 4s orbital.
l = 1 ml = ŌĆō1, 0, +1 ; three 4p orbitals.
l = 2 ml = ŌĆō2, ŌĆō1, 0, +1, +2 ; five 4d orbitals.
l = 3 ml = -3, ŌĆō2, ŌĆō1, 0, +1, +2 , +3; seven 4f orbitals
Over all Sixteen orbitals.
4s,
4p, 4d and 4f orbitals = 1 + 3 + 5 + 7
=
16 Orbitals
28. How many radial nodes for 2s, 4p, 5d and 4f orbitals exhibit? How many angular nodes?
Answer:
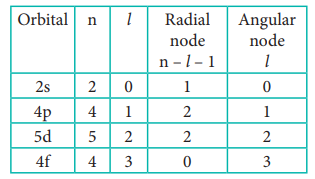
29. The stabilisation of a half filled d - orbital is more pronounced than that of the p-orbital why?
"More
exchange energy, increases the stability of orbitals"
Over
all electron exchange for d - Orbitals = 10
Over
all electron exchange for p - Orbitals = 6
Hence,
Half filled d - orbitals are more stable.
30. Consider the following electronic arrangements for the d5 configuration.

(i) which of these represents the ground state
(ii) which configuration has the maximum exchange energy.
Answer:

i)
(c) represents the ground state among the given three d5 electronic
arrangements.
ii)
Also, (c) has the maximum exchange energy.
31. State and explain pauli's exclusion principle.
No
two electrons in an atom can have the same set of values of four quantum
numbers.
32. Define orbital? what are the n and l values for 3px and 4dx2-y2 electron?
Answer:
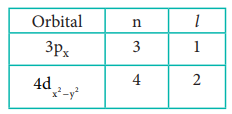
Orbital is a three dismerisional space in which the probability of finding the electron is maximum
33. Explain briefly the time independent schrodinger wave equation?
Based
on the Heisenberg's principle and the dual nature of the microscopic particles,
Schrodinger expressed the wave nature of electron in terms of a differential
equation.
This
equation determines the change of wave function in space depending on the field
of force in which the electron moves.

This
equation does not contain time (t) as a variable and is reffered to as time
independent Schordinger wave equation.
34. Calculate the uncertainty in position of an electron, if ╬öv = 0.1% and Žģ = 2.2 x106 ms-1
Answer:
Given: Δ = 0.1%
V
= 2.2 ├Ś 106 msŌłÆ1.
ΔV
= [0.1 / 100] ├Ś 2.2 ├Ś 106 msŌłÆ1= 2.2 ├Ś 103
msŌłÆ1
Solution:
Δx.m.Δv
Ōēź h/4ŽĆ
Δ
├Ś 9.1├Ś10ŌłÆ31Kg ├Ś 2.2 ├Ś 103 msŌłÆ1 Ōēź [(6.626 ├Ś 10 ŌłÆ34
) / 4ŽĆ ] Kgm2 sŌłÆ1
Δx
Ōēź ( 6.626 ├Ś 10ŌłÆ34 Kgm2 sŌłÆ1 ) / (9.1├Ś10ŌłÆ31Kg
├Ś 2.2 ├Ś 103 ms1 ├Ś 4ŽĆ)
Ōēź
( 6.626 ├Ś 10ŌłÆ34 ) / ( 251.45 ├Ś 10ŌłÆ28 ) = 0.02635 ├Ś 10-6
Δx
Ōēź 2.635 ├Ś 10-8 m
[Alternative Answer]

35. Determine the values of all the four quantum numbers of the 8th electron in O- atom and 15th electron in Cl atom and the last electron in chromium
Answer:
The
8th electron of O - atom is present in 2Px orbital

The 15th electron of Cl atom is present in 3Pz orbital

[Alternative Answer]

36. The quantum mechanical treatment of the hydrogen atom gives the energy value:
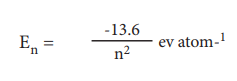
i) use this expression to find ΔE between n = 3 and m=4
ii) Calculate the wavelength corresponding to the above transition.
Answer:
(i)
E3 = ŌłÆ 13.6 / 32 = ŌłÆ1.51 eV atomŌłÆ1
En = ŌłÆ 13.6 / n┬▓ = eV
atomŌłÆ1
E4
= ŌłÆ 13.6 / 4┬▓ = ŌłÆ0.85 eV atomŌłÆ1
ΔE
= (E4 ŌĆō E3) = (ŌłÆ 0.85) ŌĆō (ŌłÆ1.51) = 0.66 eV atomŌłÆ1
(ii)
Energy difference ╬öE = 0.66 eVatomŌłÆ1
=
0.66 ├Ś 1.6 ├Ś 10ŌłÆl9J
=
1.06 ├Ś 10ŌłÆ19J
=
h╬│
h
(c/╬╗) = 1.06 ├Ś10ŌłÆ19 J
╬╗
= (hc) / (1.06 ├Ś 10ŌłÆ19) J
=
(6.626 ├Ś 10ŌłÆ34JS ├Ś 3├Ś 108msŌłÆ1 ) / ( 1.06 ├Ś 10ŌłÆ19
) J
╬╗ = 1.875├Ś l0ŌłÆ6 m
37. How fast must a 54g tennis ball travel in order to have a de Broglie wavelength that is equal to that of a photon of green light 5400├ģ?
Answer:
╬╗
= 5400A0 = 5400 ├Ś 10ŌłÆ10 m ; m = 54g
╬╗ = 54 ├Ś 10ŌłÆ3 Kg ;
V = ?
╬╗ = h / mV ;
V
= h/m╬╗
=
[ 6.626 ├Ś10ŌłÆ34 Kgm2sŌłÆ1 ] / [ 54├Ś 10ŌłÆ3
Kg ├Ś 5400 ├Ś 10ŌłÆ10 m]
V = 2.27 ├Ś 10ŌłÆ26 msŌłÆ1
38. For each of the following, give the sub level designation, the allowable m values and the number of orbitals
i) n = 4, l =2, ii) n =5, l = 3 iii) n=7, l=0
Answer:

39. Give the electronic configuration of Mn2+ and Cr3+
Electronic
configuration of Mn2+ and Cr3+
25Mn2+
(23 eŌłÆS): 1s22s2 2p6 3s23p64s03d5
24Cr3+
(21 eŌłÆS): ls22s22p63s23p64s03d3
40. Describe the Aufbau principle
In
the ground state of the atoms, the orbitals are filled in the order of their
increasing energies.
That
is once the lower energy orbitals are completely filled that the electrons
enter the next higher energy orbitals.
41. An atom of an element contains 35 electrons and 45 neutrons. Deduce
i) the number of protons
ii) the electronic configuration for the element
iii) All the four quantum numbers for the last electron
Answer:
An
atom of an element contains 35 electrons and 45 neutrons having
1)
The number of protons = 35
ii)
The electronic configuration
=
1s2 2s2 2p6 3s2 3p6 4s2
3d104p5
iii)
Four quantum numbers of the last electron
(4p5) 
n = 4; l = 1; m = 0; s = ŌłÆ1/2
[Alternative Answer]

42. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wave length associated with the electron revolving arround the nucleus.
To
Prove
"The
Circumference of the circular orbit is an integral multiple of wave
length"
That
is,
Circumference
2ŽĆr = n╬╗
If
n = 5, 2ŽĆr = 5╬╗
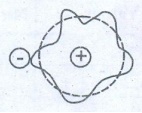
43. Calculate the energy required for the process.
He+ (g) ŌåÆ He2+ (g) + e-
The ionisation energy for the H atom in its ground state is - 13.6 ev atom-1.
Answer:

[Alternative Answer]
He+(g)
ŌåÆ He2+(g) + eŌłÆ E=
?
(Ionisation
energy of H is = 13.6 eVatomŌłÆ1)
En
= ŌłÆ13.6Z2 / n2
E1
= [ŌłÆ13.6 / 12 ] ├Ś (2)2 = ŌłÆ56.4ev
(Ōł┤Atomic
number of He = 2)
E╬▒
= [ŌłÆ13.6 ├Ś (2)2 ] / Ōł×2 = 0 ev
The
required energy of the process = EŌł× ŌłÆ E1
= 0 ŌłÆ (ŌłÆ56.4)
= 56.4 eV
44. An ion with mass number 37 possesses unit negative charge. If the ion contains 11.1% more neutrons than electrons. Find the symbol of the ion.
Answer:
Let
the mono negative ion with mass number 37 be 37z xŌłÆ
No
of protons + No of neutrons = 37
Let
the no of electrons = x
Ōł┤ The no
of protons = xŌłÆ1
no
of neutrons = 11. % of the no of electrons
=
x + 11.1 % x
=
x + [11.1 / 100]x
=
11.1 x
=>
(xŌłÆ1) + 11.1 x = 37
2.11x
ŌłÆ 1 = 37 => 2.11x = 38 => x = 38 / 2.11 = 18
Ōł┤ Atomic
number Z = No .of Protons =
= x ŌłÆ 1 = 17
Hence,
The given ion is 3717ClŌłÆ
[Alternative Answer]

45. The Li2+ ion is a hydrogen like ion that can be described by the Bohr model. Calculate the Bohr radius of the third orbit and calculate the energy of an electron in 4th orbit.
Answer:
BohrŌĆÖs
radius ╬│n = [ 0.529n2 / Z ] A0
Energy
of electron En = [ ŌłÆ13.6z2/ n2 ] eV atomŌłÆ1
For
Li2+ Atomic number = 3,
and
number of electrons = 1
i)
Bohr radius for the 3rd orbit
r3
= 0529(3)2 / 3 = l.587 A0
ii)
Energy of an electron in the 4th Orbit
E4 = (ŌłÆ13.6(3)2 ) / 42 = ŌłÆ7.65 eV atomŌłÆ1
46. Protons can be accelerated in particle accelerators. Calculate the wavelength (in ├ģ) of such accelerated proton moving at 2.85 ├Ś108 ms-1 ( the mass of proton is 1.673 ├Ś 10-27 Kg).
Answer:
V=
2.85 ├Ś l08 msŌłÆ1
mp=
1.673 ├Ś 10ŌłÆ27 kg
╬╗
= ?
╬╗
= h / mv
=
[ 6.626 ├Ś 10ŌłÆ34Kg m2sŌłÆ1 ] / [1.673 ├Ś 10ŌłÆ27Kg
├Ś 2.85 ├Ś 108msŌłÆ1 ]
=
[ ( 6.626 ) / ( 1.673├Ś 2.8 ) ]├Ś 10ŌłÆ15 m
╬╗
= 1.389 ├Ś 10ŌłÆ15m (or) 1.389 ├Ś 10-5 A0
47. What is the de Broglie wavelength (in cm) of a 160g cricket ball travelling at140 Km hr-1.
Answer:
V
= 140 kmhrŌłÆ1 = [(140 ├Ś 1000) / 3600] msŌłÆ1 = 38.88msŌłÆ1
m
= 160 g = 160 ├Ś l0ŌłÆ3 Kg;
Solution
: ╬╗ = h / mv
=
[6.626 ├Ś 10ŌłÆ34Kgm2sŌłÆ1 ] / [ 160 ├Ś 10ŌłÆ3Kg
├Ś 38.88msŌłÆ1]
=
[(6.626) / (160 ├Ś 38.88)] ├Ś 10ŌłÆ31m
=
1.065├Ś 10ŌłÆ34 m
╬╗ = 1.065├Ś 10ŌłÆ32cm
48. Suppose that the uncertainty in determining the position of an electron in an orbit is 0.6 ├ģ. What is the uncertainty in its momentum?
Answer:
Δx
= 0.6A0 ;
Δ
p = ?
Δx
╬öp Ōēź h / 4ŽĆ
0.6
├Ś 10ŌłÆ10m ├Ś ╬ö p Ōēź (6.626 ├Ś 10ŌłÆ34 ) / 4ŽĆ
Δp
Ōēź [ ( 6.626 ├Ś 10ŌłÆ34 ) / ( 0.6 ├Ś 10ŌłÆ10 ├Ś 4ŽĆ) ] Kgm2sŌłÆ1
╬öp Ōēź 0.879 ├Ś 10ŌłÆ24 KgmsŌłÆ1
49. Show that if the measurement of the uncertainty in the location of the particle is equal to its de Broglie wavelength, the minimum uncertainty in its velocity is equal to its velocity / 4ŽĆ
Answer:
If,
Δx = λ Then V = ?
Δx
╬öp Ōēź h / 4ŽĆ
╬╗
m ╬öV Ōēź h/4ŽĆ
ŌćÆ ╬öV Ōēź h / 4ŽĆ(m╬╗)
ŌćÆ ╬öV Ōēź h / [4ŽĆm(h/mv)]
(as ╬╗=h/mv)
ŌćÆ ╬öV Ōēź V / 4ŽĆ (Proved)
[Alternative Answer]
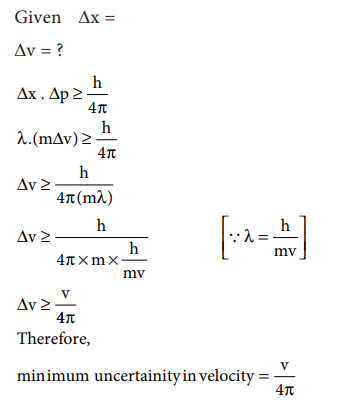
50. What is the de Broglie wave length of an electron, which is accelerated from the rest, through a potential difference of 100V?
Answer:
Potential
difference = 100V
=
100 ├Ś l.6 ├Ś l0ŌłÆ19 J = 1.6 ├Ś 10ŌłÆ17J

╬╗
= ?
╬╗=
h / ŌłÜ(2meV)
=
[ 6.26 ├Ś 10ŌłÆ34 Kgm2sŌłÆ1 ] / ŌłÜ[ 2├Ś9.1├Ś10ŌłÆ31Kg
├Ś 1.6├Ś10ŌłÆ17J ]
=
[ 6.26 ├Ś 10ŌłÆ34] / ŌłÜ[ 29.12├Ś10ŌłÆ48]
=
[ 6.26 ├Ś 10ŌłÆ34] / [ 5.4├Ś10ŌłÆ24]
╬╗
= 1.227 ├Ś 10ŌłÆ10 m (or) 1.227A0
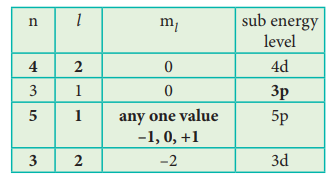
51. Identify the missing quantum numbers and the sub energy level

Answer:
Related Topics