Heisenberg’s uncertainty principle

Heisenberg’s uncertainty principle

The dual nature of matter imposes a limitation on the simultaneous determination of position and velocity of a microscopic particle. Based on this, Heisenberg arrived at his uncertainty principle, which states that ‘It is impossible to accurately determine both the position as well as the momentum of a microscopic particle simultaneously’. The product of uncertainty (error) in the measurement is expressed as follows.

Δx.Δp ≥ h/4Ï€ --------                                                                                                      (2.11)

where Δx and Δp are uncertainties in determining the position and momentum, respectively.

The uncertainty principle has negligible effect for macroscopic objects and becomes significant only for microscopic particles such as electrons. Let us understand this by calculating the uncertainty in the velocity of the electron in hydrogen atom. (Bohr radius of 1^st orbit is 0.529 Ǻ) Assuming that the position of the electron in this orbit is determined with the accuracy of 0.5 % of the radius

Uncertainity in position = ∆x

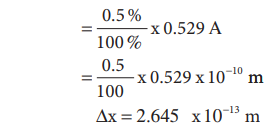
From the Heisenberg’s uncertainity principle,

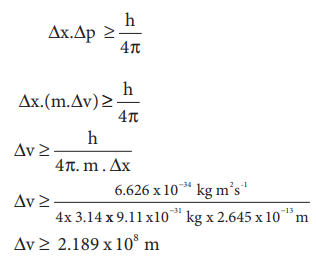
Therefore, the uncertainty in the velocity of the electron is comparable with the velocity of light. At this high level of uncertainty it is very difficult to find out the exact velocity.