Filling of orbitals

Filling of orbitals:

In an atom, the electrons are filled in various orbitals according to aufbau principle, Pauli exclusion principle and Hund's rule. These rules are described below.

Aufbau principle:

The word Aufbau in German means 'building up'. In the ground state of the atoms, the orbitals are filled in the order of their increasing energies. That is the electrons first occupy the lowest energy orbital available to them.

Once the lower energy orbitals are completely filled, then the electrons enter the next higher energy orbitals. The order of filling of various orbitals as per the Aufbau principle is given in the figure 2.12 which is in accordance with (n+l) rule.

Pauli Exclusion Principle :

Pauli formulated the exclusion principle which states that "No two electrons in an atom can have the same set of values of all four quantum numbers." It means that, each electron must have unique values for the four quantum numbers (n, l, m and s).

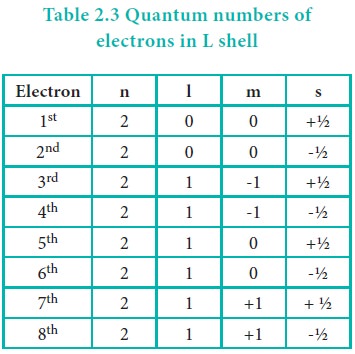
For the lone electron present in hydrogen atom, the four quantum numbers are: n = 1; l = 0; m = 0 and s = +½. For the two electrons present in helium, one electron has the quantum numbers same as the electron of hydrogen atom, n = 1, l = 0, m = 0 and s = +½. For other electron, the fourth quantum number is different i.e., n = 1, l = 0, m = 0 and s = –½.

As we know that the spin quantum number can have only two values +½ and –½, only two electrons can be accommodated in a given orbital in accordance with Pauli exclusion principle. Let us understand this by writing all the four quantum numbers for the eight electron in L shell.

Hund's rule of maximum multiplicity

The Aufbau principle describes how the electrons are filled in various orbitals. But the rule does not deal with the filling of electrons in the degenerate orbitals (i.e. orbitals having same energy) such as p_x, p_y and p_z. In what order these orbitals to be filled? The answer is provided by the Hund's rule of maximum multiplicity. It states that electron pairing in the degenerate orbitals does not take place until all the available orbitals contains one electron each.

We know that there are three p orbitals, five d orbitals and seven f orbitals. According to this rule, pairing of electrons in these orbitals starts only when the 4^th, 6^th and 8^th electron enters the p, d and f orbitals respectively.

For example, consider the carbon atom which has six electrons. According to Aufbau principle, the electronic configuration is 1s², 2s², 2p²

It can be represented as below,

In this case, in order to minimise the electron-electron repulsion, the sixth electron enters the unoccupied 2p_y orbital as per Hunds rule. i.e. it does not get paired with the fifth electron already present in the 2P_x orbital.

Electronic configuration of atoms

The distribution of electrons into various orbitals of an atom is called its electronic configuration. It can be written by applying the aufbau principle, Pauli exclusion principle and Hund's rule. The electronic configuration is written as nl^x , where n represents the principle of quantum number, 'l' represents the letter designation of the orbital [s(l=0), p (l=1), d(l=2) and f(l=3)] and 'x' represents the number of electron present in that orbital.

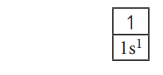
Let us consider the hydrogen atom which has only one electron and it occupies the lowest energy orbital i.e. 1s according to aufbau principle. In this case n=1; l=s; x=1.

Hence the electronic configuration is 1s¹. (spoken as one-ess-one).

The orbital diagram for this configuration is,

The electronic configuration and orbital diagram for the elements upto atomic number 10 are given below :

The actual electronic configuration of some elements such as chromium and copper slightly differ from the expected electronic configuration in accordance with the Aufbau principle.

For chromium - 24

Expected configuration :

1s² 2s² 2p⁶ 3s² 3p⁶ 3d⁴ 4s²

Actual configuration :

1s² 2s² 2p⁶ 3s² 3p⁶ 3d⁵ 4s¹

For copper - 29

Expected configuration :

1s² 2s² 2p⁶ 3s² 3p⁶ 3d⁹ 4s²

Actual configuration :

1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s¹

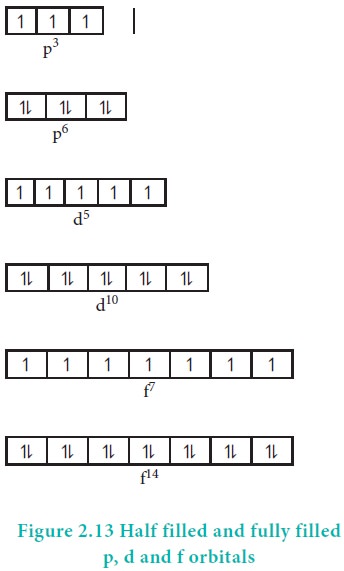
The reason for above observed configuration is that fully filled orbitals and half filled orbitals have been found to have extra stability. In other words, p³, p⁶, d⁵, d¹⁰, f⁷ and f ¹⁴ configurations are more stable than p², p⁵, d⁴, d ⁹, f⁶ and f¹³. Due to this stability, one of the 4s electrons occupies the 3d orbital in chromium and copper to attain the half filled and the completely filled configurations respectively.

Stability of half filled and completely filled orbitals:

The exactly half filled and completely filled orbitals have greater stability than other partially filled configurations in degenerate orbitals. This can be explained on the basis of symmetry and exchange energy. For example chromium has the electronic configuration of [Ar]3d⁵ 4s¹ and not [Ar]3d⁴ 4s² due to the symmetrical distribution and exchange energies of d electrons.

Symmetrical distribution of electron:

Symmetry leads to stability. The half filled and fully filled configurations have symmetrical distribution of electrons (Figure 2.13) and hence they are more stable than the unsymmetrical configurations.

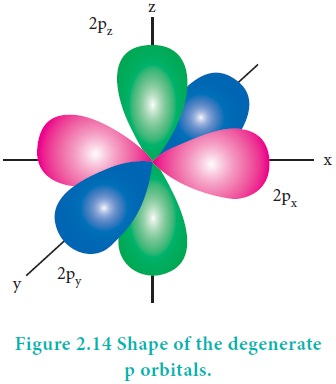
The degenerate orbitals such as p_x, p_y and p_z have equal energies and their orientation in space are different as shown in Figure 2.14. Due to this symmetrical distribution, the shielding of one electron on the other is relatively small and hence the electrons are attracted more strongly by the nucleus and it increases the stability.

Exchange energy:

If two or more electrons with the samespinarepresentindegenerateorbitals, there is a possibility for exchanging their positions. During exchange process the energy is released and the released energy is called exchange energy. If more number of exchanges are possible, more exchange energy is released. More number of exchanges are possible only in case of half filled and fully filled configurations.

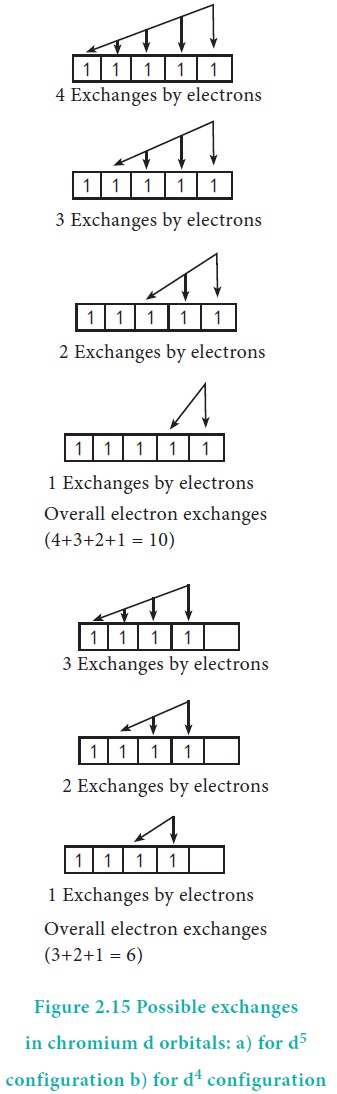
For example, in chromium the electronic configuration is [Ar]3d⁵ 4s¹. The 3d orbital is half filled and there are ten possible exchanges as shown in Figure 2.15. On the other hand only six exchanges are possible for [Ar]3d⁴ 4s² configuration. Hence, exchange energy for the half filled configuration is more. This increases the stability of half filled 3d orbitals.

The exchange energy is the basis for Hund's rule, which allows maximum multiplicity, that is electron pairing is possible only when all the degenerate orbitals contain one electron each.