Similar Triangles

Similar Triangles

Consider two given triangles PQR and ABC. They are said to be similar (~) if their corresponding angles are equal and corresponding sides are proportional. That is ∠P = ∠A, ∠Q = ∠B and ∠R = ∠C and also PQ/AB = PR/AC = QR/BC. This is denoted as ∆PQR ~ ∆ABC .

There are 4 ways by which one can prove that two triangles are similar.

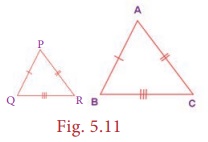
(i) AAA (Angle – Angle – Angle) or AA (Angle – Angle) Similarity

Two triangles are similar if two angles of one triangle are equal respectively to two angles of the other triangle. In the given figure, ∠A = ∠P , ∠B = ∠Q .

Therefore, ∆ABC ~ ∆PQR.

(ii) SAS (Side – Angle – Side) Similarity

Two triangles are similar if two sides of one triangle are proportional to two sides of the other triangle and the included angles are equal. In the given figure, AC/PQ = AB/PR and ∠A = ∠P and hence ∆ACB ~ ∆PQR.

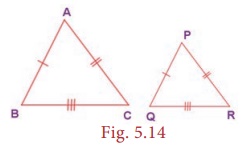
(iii) SSS (Side-Side-Side) Similarity

Two triangles are similar if their corresponding sides are in the same ratio. That is, if AB/PQ = AC/PR = BC/QR , then ∆ABC ~ ∆PQR.

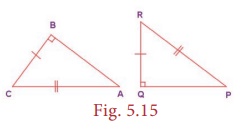
(iv) RHS (Right Angle – Hypotenuse – Side) Similarity

Two right triangles are similar if the hypotenuse and a leg of one triangle are respectively proportional to the hypotenuse and a leg of the other triangle. That is, if ∠B = ∠Q = 90º and AC/PR = BC/QR  then, ∆ABC ~ ∆PQR.

 If ∆ABC ~ ∆PQR, then the corresponding sides to AB, BC and AC of ∆ABC are PQ, QR and PR respectively and the corresponding angles to A, B and C are P, Q and R respectively. Naming a triangle has a significance. For example, if ∆ABC ~ ∆PQR then, ∆BAC is not similar to ∆PQR.

Example 5.5

In the Fig. 5.16, if ∆PQR ~ ∆XYZ , find a and b.

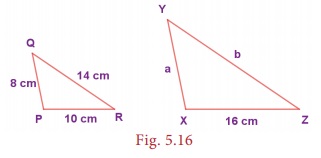
Solution:

Given that ∆PQR ~ ∆XYZ

Their corresponding sides are proportional.

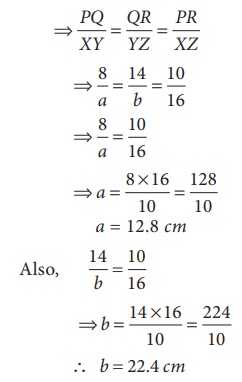
∴ b = 22.4 cm

Note

• All circles and squares are similar to each other.

• Not all rectangles need to be similar always.

• If two angles are both congruent and supplementary then, they are right angles.

• All congruent triangles are similar.

• The symbol ~ is used to denote similarity.

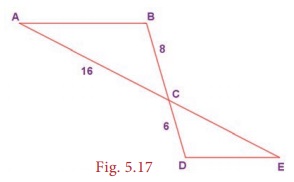
Example 5.6 (Illustrating AA Similarity)

In the Fig. 5.17 , ∠ABC ≡ ∠EDC and the perimeter of ∆CDE is 27 units, prove that AB ≡ EC.

Proof:

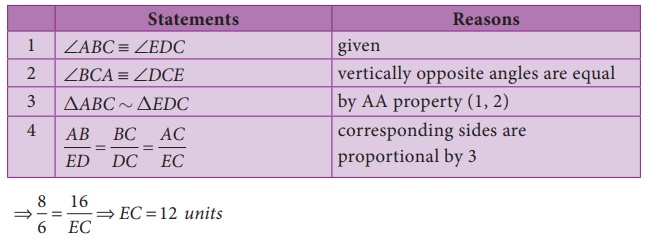
⇒ 8/6 = 16/EC

⇒ EC =12 units

Given, the perimeter of ∆CDE = 27 units,

 ED + DC + EC = 27

⇒ ED + 6 + 12 = 27

⇒ ED = 27–18 = 9 units

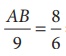
 AB/9 = 8/6 ⇒ AB = 12 units and hence AB = EC.

Example 5.7 (Illustrating AA Similarity)

In the given Fig. 5.18, if ∠1 ≡ ∠3 and ∠2 ≡ ∠4 then, prove that ∆BIG ~ ∆FAT . Also find FA.

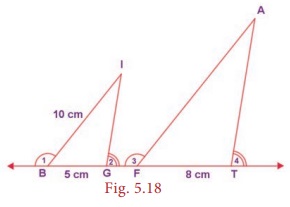
Proof:

Also, their corresponding sides are proportional

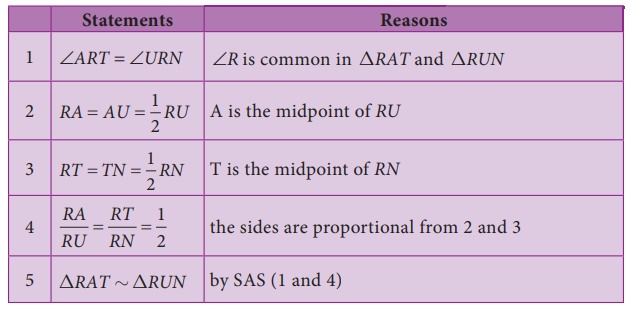
Example 5.8 (Illustrating SAS Similarity)

If A is the midpoint of RU and T is the midpoint of RN, prove that ∆RAT ~ ∆RUN .

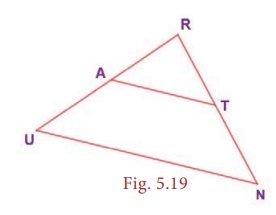
Proof:

Example 5.9 (Illustrating SSS similarity)

Prove that ∆PQR ~ ∆PRS in the given Fig. 5.20.

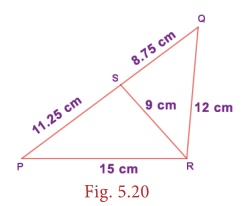
Solution:

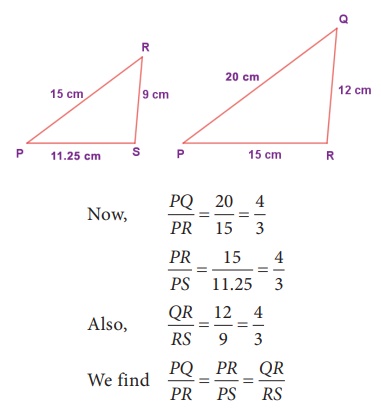
That is, their corresponding sides are proportional.

By SSS Similarity, ∆PQR ~ ∆PRS

Example 5.10 (Illustrating RHS similarity)

The height of a man and his shadow form a triangle similar to that formed by a nearby tree and its shadow. What is the height of the tree?

Solution:

Here, ∆ABC ~ ∆ADE (given)

Their corresponding sides are proportional (by RHS similarity).

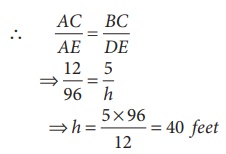
⇒ h = [5×96] / 12 = 40 feet

 The height of the tree is 40 feet.

Activity

The teacher cuts many triangles that are similar or congruent from a card board (or) chart sheet. The students are asked to find which pair of triangles are similar or congruent based on the measures indicated in the triangles.