Construction of Special Quadrilaterals

Construction of Special Quadrilaterals

Before we begin to learn constructing certain quadrilaterals, it is essential to recall their basic properties that would help us during the process. We will try to do this by performing some activities and then sum them up.

Activity

1. Place a pair of unequal sticks (say pieces of broomstick) such that they have their end points joined at one end.

2. Now place another such pair meeting the free ends of the first pair.

What is the figure enclosed? It is a quadrilateral. Name it as ABCD. How many sides are there? What are its diagonals? Are the diagonals equal? Are the angles equal?

In the above activity can you get a quadrilateral in which

(i) All the four angles are acute.

(ii) One of the angles is obtuse.

(iii) Two of the angles are obtuse.

(iv) One of the angles is a right angle.

(v) Two of the angles are right angles.

(vi) The diagonals are mutually ┴^r.

Activity

1. A pair of identical 30º–60º –90º set-squares are needed for this activity. Place them as shown in the figure.

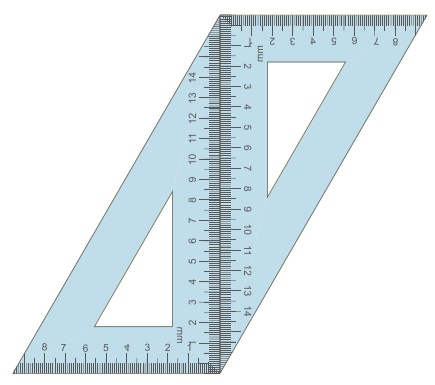
(i) What is the shape we get? It is a parallelogram.

(ii) Are the opposite sides parallel? − Answer: Yes

(iii) Are the opposite sides equal? − Answer: Yes

(iv) Are the diagonals equal? − Answer: No

(v) Can you get this shape by using any other pair of identical set-squares? − Answer: Yes

2. We need a pair of 30º–60º –90º  set- squares for this activity. Place them as shown in the figure.

(i) What is the shape we get? − Answer: Rectangle

(ii) Is it a parallelogram? Answer: Yes

It is a quadrilateral; infact it is a rectangle. (How?) Answer: Opposits sides are equal.  All angles = 90°

(iii) What can we say about its lengths of sides, angles and diagonals?

Discuss and list them out.

Answer:

Opposite sides are equal

All angles are equat and are = 90°

Diagonals are equal

3. Repeat the above activity, this time with a pair of 45º–45º–90º set-squares.

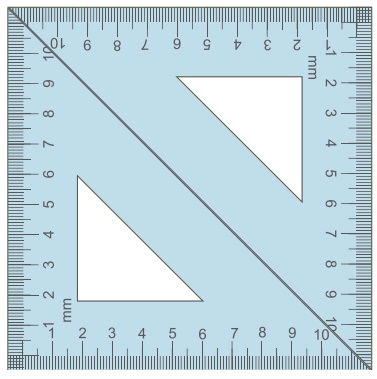
(i) How does the figure change now? Is it a parallelogram? It becomes a square! (How did it happen?)

Answer: All sides are equal. So it is square.

(ii) What can we say about its lengths of sides, angles and diagonals?

Discuss and list them out.

Answer:

All sides are equal

All angles = 90°

Diagonals equal

(iii) How does it differ from the list we prepared for the rectangle?

Answer:

All sides are equal.

Diagonals bisects each other.

4. We again use four identical 30º –60º –90º set- squares for this activity. Note carefully how they are placed touching one another.

(i) Do we get a parallelogram now? Answer: Yes

(ii) What can we say about its lengths of sides, angles and diagonals?

Answer:

All sides equal.

opposite sides are equal and parallel.

(iii) What is special about their diagonals?

Answer: Diagonals bisects perpendicularly.

Based on the outcome of the above activities, we can list out the various properties of the above quadrilaterals, all of which happen to be parallelograms!

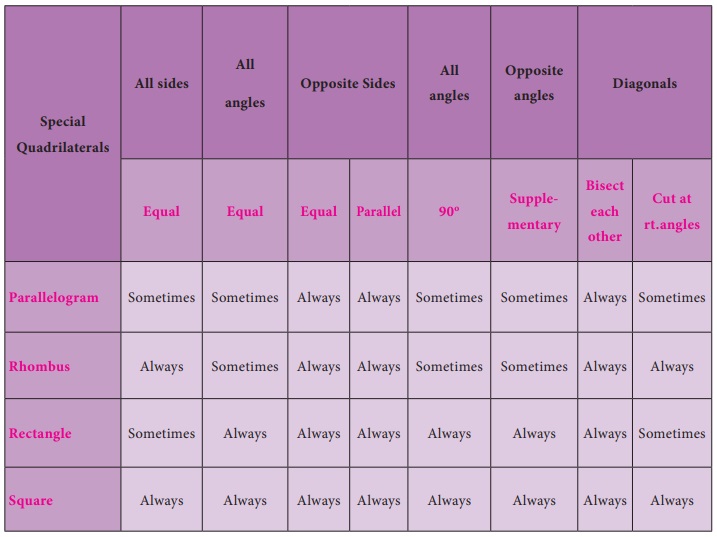
Try these

1. Say True or False:

(a) A square is a special rectangle. [Answer: True]

(b) A square is a parallelogram. [Answer: True]

(c) A square is a special rhombus. [Answer: True]

(d) A rectangle is a parallelogram [Answer: False]

2. Name the quadrilaterals

(a) which have diagonals bisecting each other.

Answer: Square, rectangle, parallelogram, rhombus.

(b) In which the diagonals are perpendicular bisectors of each other.

Answer: Rhombus and square.

(c) Which have diagonals of different lengths.

Answer: Parallelogram and Rhombus

(d) Which have equal diagonals.

Answer: Square.

(e) Which have parallel opposite sides.

Answer: Square, Rectangle, Rhombus, parallelogram.

(f) In which opposite angles are equal.

Answer: Square, rectangle.

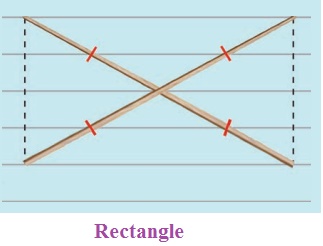
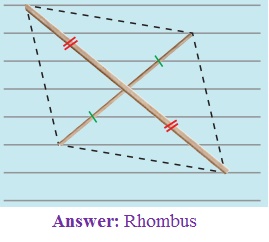
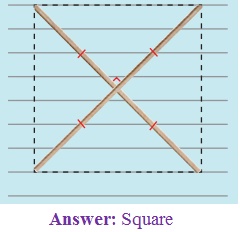
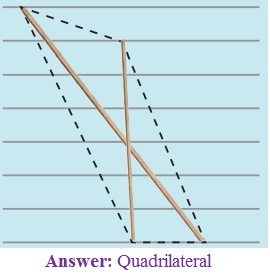
3. Two sticks are placed on a ruled sheet as shown. What figure is formed if the four corners of the sticks are joined?

(a) Two unequal sticks. Placed such that their midpoints coincide.

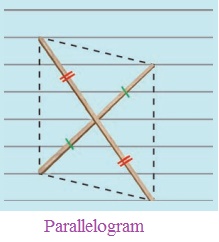
(b) Two equal sticks. Placed such that their midpoints coincide.

(c) Two unequal sticks. Placed intersecting at mid points perpendicularly.

(d) Two equal sticks. Placed intersecting at mid points perpendicularly.

(e) Two unequal sticks. Tops are not on the same ruling. Bottoms on the same ruling. Not cutting at the mid point of either.

(f) Two unequal sticks. Tops on the same ruling. Bottoms on the same ruling. Not necessarily cutting at the mid point of either.

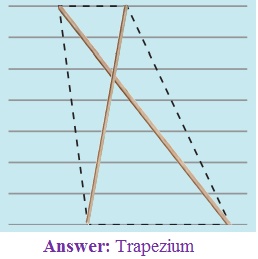
Answer:

(a) parallelogram

(b) Rectangle

(c) Rhombus

(d) Square

(e) Quadrilateral

(f) Trapezium