Exercise 5.3

Exercise 5.3

Miscellaneous Practice Problems

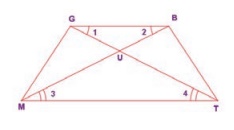
1. In the figure, given that ∠1 ≡ ∠2 and ∠3 ≡ ∠4 . Prove that ∆ MUG ≡ ∆TUB.

Solution:

Proof:

Statements: Reasons

1. In ΔMUG and ΔTUB

MU = TU : ∠3 = ∠4, opposite sides of equal angles

2. UG = UB : ∠1 = ∠2

Side opposite to equal angles are equal

3. ∠GUM = ∠BUT : Vertically opposite angle

4. ΔMUG ≡  ΔTUB : SAS criteria By 1, 2 and 3

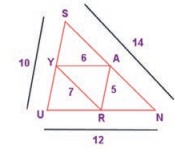
2. From the figure, prove that ∆SUN ~ ∆RAY.

Solution:

Proof: from the ΔSUN and ΔRAY

SU = 10

UN = 12

SN = 14

RA = 5

AY = 6

RY = 7

We have 

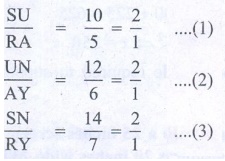
SU/RA = 10/5 = 2/1    …….(1)

UN/AY = 12/6 = 2/1      …….(2)

SN/RY = 14/7 = 2/1      …….(3)

From (1), and (2) and (3) we have

SU/RA = UN/AY = SN/RY = 2/1

The sides are proportional

  ∴   ΔSUN ~ Δ RAY

3. The height of a tower is measured by a mirror on the ground at R by which the top of the tower’s reflection is seen. Find the height of the tower. If ∆PQR ~ ∆STR

Solution:

The image and its reflection make similar shapes

Δ PQR ~ Δ STR

PQ/ST = QR/TR =PR/SR

= 48 feet

∴ Height of the tower = 48 feet.

4. Find the length of the support cable required to support the tower with the floor.

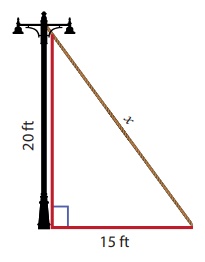
Solution:

From the figure, by Pythagoras theorem,

x² = 20² + 15²

= 400 + 225 = 625

x² = 25² ⇒ x = 25ft.

∴ The length of the support cable required to support the tower with the floor is 25 ft.

5. Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason.

Solution:

Take the sides of a right angled triangle ΔABC as

a = 7 inches

b = 25 inches

c = ?

By Pythagoras theorem,

b² = a² + c²

25² = 7² + c²

⇒ c² = 25² − 7² = 625 − 49 = 576

c² = 24²

=> c = 24 inches

∴ Width of TV cabinet is 20 inches which is lesser than the width of the screen ie.24 inches.

∴ The TV will not fit into the cabinet.

Challenging problems

6. In the figure, ∠TMA ≡ ∠IAM and ∠TAM ≡ ∠IMA . P is the midpoint of MI and N is the midpoint of AI. Prove that ∆ PIN ~ ∆ ATM.

Solution:

Proof:

Statements: Reasons

1. ∠TMA = ∠IAM

∠TAM = ∠IMA  : Reasons: given

2. ∠ATM = ∠TIM : Reasons: Remaining angle

By angle sum property

3. IP = PM ⇒ = IP/PM = 1

In = NA ⇒ = IN/NA = 1 : Reasons: P is the midpoint of IM and N is the midpoint of IA

4. IP / PM = IN / NA  :  Reasons: By 3

5. PN || MA : Reasons: By 4

6. ∠IPN = ∠IMN

∠INP = ∠IAM   :   Reasons: By 5

7. In ΔPIN and ΔATM

(i) ∠IPN = ∠TAM

(ii) ∠INP = ∠TMA

(iii) ∠ATM = ∠PIN  : Reasons: By 1, 2 and 6

8. ΔPIN ~ ΔATM   :  Reasons: By AAA criteria

7. In the figure, if ∠FEG ≡ ∠1 then, prove that DG ² = DE . DF .

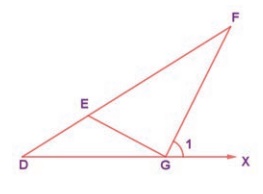
Solution:

Proof:

Statements : Reasons

1. ∠FEG ≡ ∠1

⇒ ∠DEG = 180° − ∠FEG  

Reasons:

Given

linear pair

2. ∠FDG + ∠DFG = 1

∠EDG + ∠DFG = 1

Reasons: Exterior angle = Sum of interior opposite angles

∵ ∠FDG = ∠EDG

3. ∠DEG = 180° − ∠FEG

∠DEG = 180 − ∠1

Reasons: By 1

4. In ΔDFG

∠DGF =180° − [∠FDG + ∠DFG]

Reasons: Angle sum property

5. ∠DGF= 180° − ∠1

Reasons: By 2

6. ∠DGF = ∠DEG

Reasons: By 3

7. ∠EDG = ∠EDG

Reasons: Common in ΔFDG and ΔEDG

8. ∴ ∠DGE = ∠DFG

Reasons: Remaining angle by angle sum property and by 6

9. ∴  ΔDGF ~ ΔDEG

Reasons: By 6, 7, 8

By AAA similarity

10. DG / DE = GF /EG = DF / DG

Reasons: Corresponding sides of similar trianlge are proportional.

11. DG / DE = DF / DG

DG. DG = DF. DE

DG² = DE.DF

Reasons: From 9

8. The diagonals of the rhombus is 12 cm and 16 cm. Find its perimeter. (Hint: the diagonals of rhombus bisect each other at right angles).

Solution:

Here AO = CO = 8 cm

BO = DO = 6 cm

(∴  the diagonals of rhombus bisect each other at right angles)

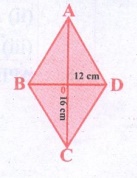
∴  In Δ AOB, AB² = AO² + OB²

= 8² + 6² = 64 + 36

= 100 = 10²

∴ AB = 10

Since it is a rhombus, all the four sides are equal.

AB = BC = CD = DA

∴ Its Perimeter = 10 + 10 + 10 + 10 = 40 cm

9. In the figure, find AR.

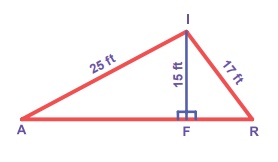
Solution: 

Δ AFI, Δ FRI are right triangles.

 By Pythagoras theorem,

 AF² = AI² − FI²

 = 25² − 15²

 = 625 − 225 = 400 = 20²

∴  AF = 20 ft.     ….(1)

 FR² = RI² − FI²

 = 17² − 15² = 289 – 225 = 64 = 8²

 FR = 8 ft.

∴ AR = AF + FR

 = 20 + 8 = 28 ft.

10. In ∆DEF, DN, EO, FM are medians and point P is the centroid. Find the following.

(i) IF DE = 44, then DM = ?

(ii) IF PD = 12, then PN = ?

(iii) If DO = 8, then FD = ?

(iv) IF OE = 36 then EP = ?

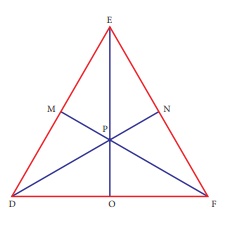
Solution:

Given DN, EO, FM are medians.

∴ FN = EN

 DO = FO

 EM = DM

(i) If DE = 44, then

DM = 44 / 2 = 22

DM = 22

(ii) If PD = 12, PN = ?

 PD / PN = 2/1

 12 / PN = 2/1 ⇒ PN = 12/2 = 6.

PN = 6

(iii) If DO = 8, then

 FD = DO + OF

 = 8 + 8

 FD = 16

(iv) IF OE = 36,

then EP / PO = 2 / 1

EP / 2 = PO

OE = OP + PE

 36 = [PE / 2] + PE

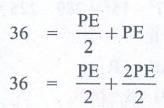
 36 = [PE / 2] +  [2PE / 2]

36 = 3PE / 2

PE = [36 × 2] / 3

PE = 24 

Answer:

Exercise 5.3

Miscellaneous Practice Problems

3. 48 ft

4. 25 ft

5. No, the wide of cabinet is lesser than the wide of TV

Challenging Problems

8. 40cm

 9. 28 ft

10. (i) 24 (ii) 6 (iii) 16 (iv) 24