Questions with Answers, Solution | Geometry | Chapter 5 | 8th Maths - Exercise 5.2 (Triangle) | 8th Maths : Chapter 5 : Geometry

Chapter: 8th Maths : Chapter 5 : Geometry

Exercise 5.2 (Triangle)

8th Maths : Chapter 5 : Geometry : Exercise 5.2 : The Pythagorean Theorem, Converse of Pythagoras Theorem, Point of Concurrency, Medians of a Triangle, Altitude of a Triangle, Perpendicular Bisectors of a Triangle, Angle Bisectors of a Triangle : Text Book Back Numerical problems, Exercises Questions with Answers, Solution

Exercise 5.2

1. Fill in the blanks:

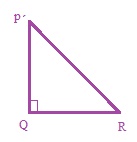
(i) If in a ∆PQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________. [Answer: Q]

Solution:

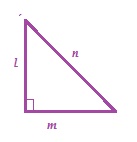
(ii) If ' l ' and ‘m’ are the legs and 'n' is the hypotenuse of a right angled triangle then, l2 = ________. [Answer: n2 − m2]

Solution:

(iii) If the sides of a triangle are in the ratio 5:12:13 then, it is ________. [Answer: a right angled triangle.]

Solution:

132 = 169

52 = 25

122 = 144

169 = 25 + 144

∴ 132 = 52 + 122

(iv) The medians of a triangle cross each other at ___________. [Answer: Centroid]

(v) The centroid of a triangle divides each medians in the ratio ___________. [Answer: 2:1]

2. Say True or False.

(i) 8, 15, 17 is a Pythagorean triplet. [Answer: True]

Solution:

172 = 289

152 = 225

82 = 64

64 + 225 = 289 ⇒ 172 = 152 + 82

(ii) In a right angled triangle, the hypotenuse is the greatest side. [Answer: True]

Solution:

(iii) In any triangle the centroid and the incentre are located inside the triangle. [Answer: True]

(iv) The centroid, orthocentre, and incentre of a triangle are collinear. [Answer: True]

(v) The incentre is equidistant from all the vertices of a triangle. [ Answer: False]

3. Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem.

(i) 8,15,17 (ii) 12,13,15 (iii) 30,40,50 (iv) 9,40,41 (v) 24,45,51

Solution:

(i) 8, 15, 17

Take a = 8, b = 15 and c = 17

Now a2 + b2 = 82 + 152 = 64 + 225 = 289

172 = 289 = c2

∴ a2 + b2 = c2

By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.

∴ Answer : yes.

(ii) 12, 13, 15

Take a = 12, b = 13 and c = 15

Now a2 + b2 = 122 + 132 = 144+ 169 = 313

152 = 225 ≠ 313

By the converse of Pythagoras theorem, the triangle with given measures is not a right angled triangle.

∴ Answer : No.

(iii) 30, 40, 50

Take a = 30, b = 40 and c = 50

Now a2 + b2 = 302 + 402 = 900 + 1600 = 2500

c2 = 502 = 2500

∴ a2 + b2 = c2

By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.

∴ Answer : yes.

(iv) 9, 40, 41

Take a = 9, b = 40 and c = 41

Now a2 + b2 = 92 + 402 = 81 + 1600 = 1681

c2 = 412 = 1681

∴ a2 + b2 = c2

By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.

∴ Answer : yes.

(v) 24, 45, 51

Take a = 24, b = 45 and c = 51

Now a2 + b2 = 242 + 452 = 576 + 2025 = 2601

c2 = 512 = 2601

∴ a2 + b2 = c2

By the converse of Pyhtagoreas theorem, the triangle with given measure is a right angled triangle.

∴ Answer: yes.

4. Find the unknown side in the following triangles.

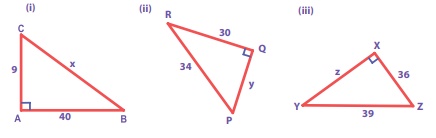
Solution:

(i) From Δ ABC, by Pythagoras theorem

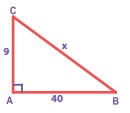
BC2 = AB2 + AC2

Take AB2 + AC2 = 92 + 402 = 81 + 1600= 1681

BC2 = AB2 + AC2 = 1681 = 412

BC2 = 412 ⇒ BC = 41

∴ x = 41

(ii) From Δ PQR, by Pythagoras theorem,

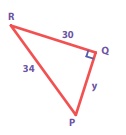
PR2 = PQ2 + QR2

342 = y2 + 302

⇒ y2 = 342 − 302

= 1156 − 900

= 256 = 162

y2 = 162 ⇒ y = 16

(iii) From ΔXYZ, by Pythagoras theorem,

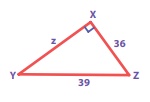
YZ2 = XY2 + XZ2

⇒ XY2 = YZ2 − XZ2

Z2 = 392 − 362

= 1521 − 1296

= 225 = 152

Z2 = 152

⇒ Z = 15

5. An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height.

Solution:

In an isosceles triangle the altitude dives its base into two equal parts.

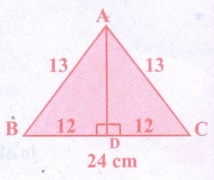
Now in the figure, ΔABC is an isosceles triangle with AD as its height

In the figure, AD is the altitude and ΔABD is a right triangle.

By Pythagoras theorem,

AB2 = AD2 + BD2

=> AD2 = AB2 − BD2

= 132 − 122 = 169 − 144 = 25

AD2 = 25 = 52

Height: AD = 5 cm

6. Find the distance between the helicopter and the ship.

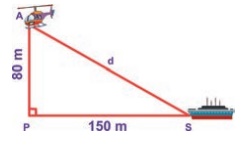
Solution:

From the figure AS is the distance between the helicopter and the ship.

ΔAPS is a right angled triangle, by Pythagoras theorem,

AS2 = AP2 + PS2

= 802 + 1502 = 6400 + 22500 = 28900 = 1702

∴ The distance between the helicopter and the ship is 170 m

7. In triangle ABC, line l1 is a perpendicular bisector of BC.

If BC=12 cm, SM=8 cm, find CS.

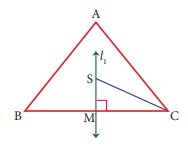
Solution:

Given l1 is the perpendicular bisector of BC.

∴ ∠SMC = 90° and BM = MC

BC = 12 cm

=> BM + MC = 12 cm [ BM = MC ]

MC + MC = 12 cm

2MC = 12

MC = 12/2

MC = 6 cm

Given SM = 8 cm

By Pythagoras theorem SC2 = SM2 + MC2

SC2 = 82 + 62

SC2 = 64 + 36

CS2 = 100

CS2 = 102

CS = 10 cm

8. Identify the centroid of ∆PQR.

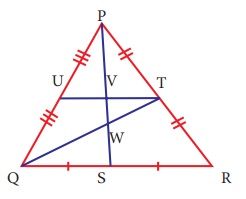
Solution:

In ΔPQR, PT = TR ⇒ QT is a median from vertex Q.

QS = SR ⇒ PS is a median from vertex P.

QT and PS meet at W and therefore W is the centroid of ΔPQR.

9. Name the orthocentre of ∆PQR.

Solution:

∠P = 90°

This is a right triangle

∴ orthocentre = P [∵ In right triangle orthocentre is the vertex containing 90°]

10. In the given figure, A is the midpoint of YZ and G is the centroid of the triangle XYZ. If the length of GA is 3 cm, find XA.

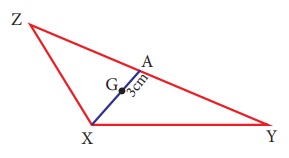
Solution:

Given A is the midpoint of YZ.

∴ ZA = AY

G is the centroid of Δ XYZ centroid divides each median in a ratio 2 : 1 ⇒ XG : GA = 2:1

XG/GA = 2/1

XG/3 = 2/1

XG = 2 × 3

XG = 6 cm

XA = XG + GA = 6 + 3 ⇒ XA = 9 cm

11. If I is the incentre of ∆XYZ, ∠IYZ = 30º and ∠IZY = 40º , find ∠YXZ .

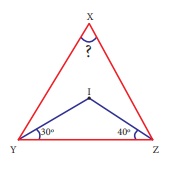
Solution:

Since I is the incentre of ΔXYZ

∠IYZ = 30° ⇒ ∠IYX = 30°

∠IZY =. 40° ⇒ ∠IZX = 40°

∴ ∠XYZ = ∠XYI + ∠IYZ = 30° + 30°

∠XYZ = 60°

||| ly ∠XYZ = ∠XZI + ∠IZY = 40° + 40°

∠XYZ = 80°

By angle sum property of a triangle

∠XZY + ∠XYZ + ∠YXZ = 180°

80° + 60° + ∠YXZ = 180°

140° + ∠YXZ = 180°

∠YXZ = 180° − 140°

∠YXZ = 40°

Objective Type Questions

12. If ∆GUT is isosceles and right angled, then ∠TUG is ____________.

(A) 30º

(B) 40º

(D) 55º

Answer: (C) 45°

Solution:

∠U ∠T = 45° (∵ Δ GUT is an isosceles given)

∴ ∠TUG = 45°

13. The hypotenuse of a right angled triangle of sides 12cm and 16cm is __________.

(A) 28 cm

(B) 20 cm

(D) 21 cm

[Answer: (B) 20 cm]

Solution:

Side take a = 12 cm

b = 16 cm

The hypotenuse c2 = a2 + b2

= 122 +162

= 144 + 256

c2 = 400 ⇒ c = 20 cm

14. The area of a rectangle of length 21cm and diagonal 29cm is __________.

(A) 609 cm2

(B) 580 cm2

(D) 210 cm2

[Answer: (C) 420 cm2]

Solution:

length = 21 cm

diagonal = 29 cm

By the converse of Pythagoras theorem,

AB2 + BC2 = AC2

212 + x2 = 292

x2 = 841 − 441 = 400 = 202

x = 20 cm

Now area of the rectangle = length × breadth.

ie AB × BC = 21 cm × 20 cm = 420 cm2

15. The sides of a right angled triangle are in the ratio 5:12:13 and its perimeter is 120 units then, the sides are ______________.

(A) 25, 36, 59

(B) 10,24,26

(D) 20,48,52

[Answer: (D) 20, 48, 52]

Solution:

The sides of a right angled triangle are in the ratio 5 : 12 : 13

Take the three sides as 5a, 12a, 13a = 30a

Its perimeter is 5a + 12a + 13a = 30a

It is given that 30a = 120 units

a = 4 units

∴ the sides 5a = 5 × 4 = 20 units

12a = 12 × 4 = 48 units

13a = 13 × 4 = 52 units

Answer:

Exercise 5.2

1. (i) Q (ii) n2 − m2 (iii) a right angled triangle (iv) centraid (v) 2:1

2. (i) True (ii) True (iii) True (iv) True (v) False

3. (i) Yes (ii) No (iii) Yes (iv) Yes (v) yes

4 (i) x = 41 (ii) y = 16 (iii) z = 15

5. 5cm

6. 170m

7. 10cm

8. W

9. P

10. 9cm

11. (c) 42 °

12. (c) 45 °

13. (b) 20cm

14. (c) 420cm2

15. (d) 20, 48, 52

Tags : Questions with Answers, Solution | Geometry | Chapter 5 | 8th Maths , 8th Maths : Chapter 5 : Geometry

Study Material, Lecturing Notes, Assignment, Reference, Wiki description explanation, brief detail

8th Maths : Chapter 5 : Geometry : Exercise 5.2 (Triangle) | Questions with Answers, Solution | Geometry | Chapter 5 | 8th Maths