Altitude of a Triangle

Altitude of a Triangle

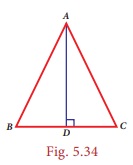
Altitude of a triangle also known as the height of the triangle, is the  perpendicular drawn from the vertex of the triangle to the opposite side.

The altitude makes a right angle with the base of a triangle. Here, in ∆ABC, AD is one of the altitudes as AD ⊥ BC.

Activity

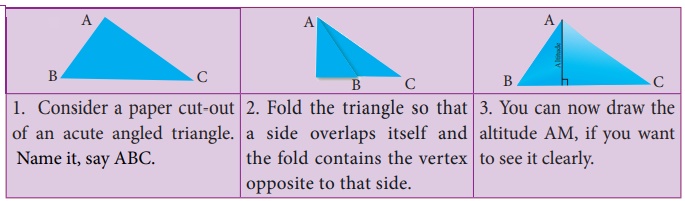
In the same way, you find altitudes of other two sides. Also, with the help of your teacher, you find altitudes of right angled triangle and obtuse angled triangle. Do the altitudes of triangle pass through the same point? What is your conclusion? We see that,

The three altitudes of any triangle are concurrent.

The point of concurrence is known as its Orthocentre, denoted by the letter H.

Think

1. In any acute angled triangle, all three altitudes are inside the triangle. Where will be the orthocentre?

 In the interior of the triangle or in its exterior?

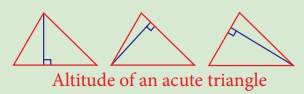
Solution: Interior of the triangle.

Altitude of an acute triangle

2. In any right angled triangle, the altitude perpendicular to the hypotenuse is inside the triangle; the other two altitudes are the legs of the triangle. Can you identify the orthocentre in this case?

Solution: Vertex containing 90°

Altitude of a right triangle

3. In any obtuse angled triangle, the altitude connected to the obtuse vertex is inside the triangle, and the two altitudes connected to the acute vertices are outside the triangle. Can you identify the orthocentre in this case?

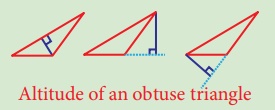
Solution: Exterior of the triangle.

Altitude of an obtuse triangle