Construction of Quadrilaterals

Construction of Quadrilaterals

We have already learnt how to draw triangles in the earlier classes. A polygon that has got 3 sides is a triangle. To draw a triangle, we need 3 independent measures. Also, there is only one way to construct a triangle, given its 3 sides. For example, to construct a triangle with sides 3cm, 5cm and 7cm, there is only one way to do it.

Now, let us move on to quadrilaterals. A polygon that is formed by 4 sides is called a quadrilateral. Isn’t it? But, a quadrilateral can be of different shapes. They need not look like the same for the given 4 measures. For example, some of the quadrilaterals having their sides as 4 cm, 5 cm, 7 cm and 9 cm are given below

So, to construct a particular quadrilateral, we need a 5^th measure. That can be its diagonal or an angle measure. Moreover, even if 2 or 3 sides are given, using the measures of the diagonals and angles, we can construct quadrilaterals.

Note

We can split any quadrilateral into two triangles by drawing a diagonal.

In the above figures, a quadrilateral is split in two ways by its diagonals. So, if a diagonal is given, first draw the lower triangle with two sides and one diagonal. Then, draw the upper triangle with other two measures.

(i) • A polygon in which atleast one interior angle is more than 180°, is called a concave polygon. In the given polygon, interior angle at C is more than 180°.

• A polygon in which each interior angle is less than 180°, is called a convex polygon. In the given polygon, all interior angles are less than 180°.

(ii) Look at the following quadrilaterals.

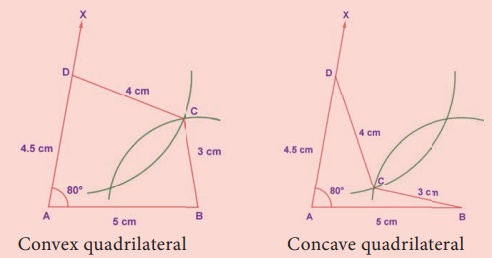
Though, we can construct a quadrilateral in two ways as shown above, we do not take into account the concave quadrilaterals in this chapter. Hence, the construction of only convex quadrilaterals are treated here.

Note

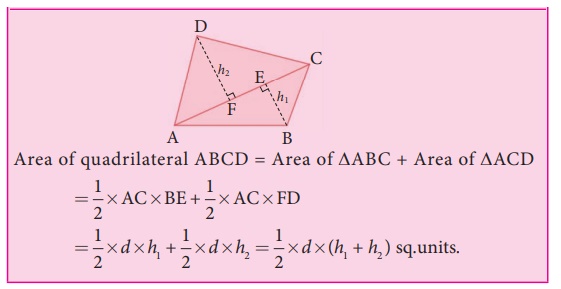
Consider the given Quadrilateral ABCD. In which AC is a diagonal (d), BE (h₁) and DF (h₂) are the perpendiculars drawn from the vertices B and D on diagonal AC.

Area of quadrilateral ABCD = Area of ∆ABC + Area of ∆ACD

We shall now see a few types on constructing these quadrilaterals when its:

(i) 4 sides and a diagonal are given.

(ii) 3 sides and 2 diagonals are given.

(iii) 4 sides and an angle are given.

(iv) 3 sides and 2 angles are given.

(v) 2 sides and 3 angles are given.

1. Constructing a quadrilateral when its 4 sides and a diagonal are given

Example 5.21

Construct a quadrilateral DEAR with DE=6 cm, EA = 5 cm, AR = 5.5cm, RD = 5.2 cm and DA = 10 cm. Also find its area.

Solution:

Given:

DE = 6 cm, EA = 5 cm, AR = 5.5 cm,

RD = 5.2 cm and a diagonal

DA = 10 cm

Steps:

4. Draw a line segment DE = 6 cm.

5. With D and E as centres, draw arcs of radii 10 cm and 5 cm respectively and let them cut at A.

6. Join DA and EA.

7. With D and A as centres, draw arcs of radii 5.2 cm and 5.5 cm respectively and let them cut at R.

8. Join DR and AR .

9. DEAR is the required quadrilateral.

2. Construct a quadrilateral when its 3 sides and 2 diagonals are given

Example 5.22

Construct a quadrilateral NICE with NI=4.5 cm, IC= 4.3 cm, NE= 3.5 cm, NC= 5.5 cm and IE = 5 cm. Also find its area.

Solution:

Given:

NI = 4.5 cm, IC= 4.3 cm,

NE = 3.5 cm and two diagonals,

NC = 5.5 cm and IE = 5 cm

Steps:

1. Draw a line segment NI = 4.5 cm.

2. With N and I as centres, draw arcs of radii 5.5 cm and 4.3 cm respectively and let them cut at C.

3. Join NC and IC.

4. With N and I as centres, draw arcs of radii 3.5 cm and 5 cm respectively and let them cut at E.

5. Join NE, IE and CE .

6. NICE is the required quadrilateral.

3. Construct a quadrilateral when its 4 sides and one angle are given

Example 5.23

Construct a quadrilateral MATH with MA=4 cm, AT= 3.6 cm, TH = 4.5 cm, MH= 5 cm and ∠A = 85º . Also find its area.

Solution:

Given:

MA=4 cm, AT= 3.6 cm,

TH = 4.5 cm, MH= 5 cm and ∠A = 85º

Steps:

1. Draw a line segment MA = 4 cm.

2. Make ∠A = 85º .

3. With A as centre, draw an arc of radius 3.6 cm. Let it cut the ray AX at T.

4. With M and T as centres, draw arcs of radii 5 cm and 4.5 cm respectively and let them cut at H.

5. Join MH and TH.

6. MATH is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral MATH = 1/2 × d × ( h₁ + h₂ ) sq. units

= 1/2 × 5.1× (3.9 + 2.8)

= 2.55 × 6.7 = 17.09 cm²

4. Construct a quadrilateral when its 3 sides and 2 angles are given

Example 5.24

Construct a quadrilateral ABCD with AB=7 cm, AD= 5 cm, CD = 5 cm, ∠BAC = 50º and ∠ABC = 60º. Also find its area.

Solution:

Given:

AB=7 cm, AD= 5 cm, CD = 5 cm and two angles ∠BAC = 50º and ∠ABC = 60º

Steps:

1. Draw a line segment AB = 7 cm.

2. At A on AB , make ∠BAY = 50º and at B on AB, make ∠ABX = 60º . Let them intersect at C.

3. With A and C as centres, draw arcs of radius 5 cm each. Let them intersect at D.

4. Join AD and CD.

5. ABCD is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral ABCD = 1/2 × d × ( h₁ + h₂ ) sq. units

= 1/2 × 6.4 × (3.8 + 5.3)

= 3.2 × 9.1 = 29.12 cm²

5. Construct a quadrilateral when its 2 sides and 3 angles are given

Example 5.25

Construct a quadrilateral PQRS with PQ=QR=5 cm, ∠QPR = 50°, ∠PRS = 40° and ∠RPS = 80°. Also find its area.

Solution:

Given:

PQ= 5 cm, QR=5 cm, ∠QPR = 50°,

∠PRS = 40° and ∠RPS = 80°

Steps:

1. Draw a line segment PQ = 5 cm.

2. At P on PQ, make ∠QPX = 50°.

3. With Q as centre, draw an arc of radius 5 cm. Let it cut PX at R.

4. At R on PR, make ∠PRS = 40° and at P on PR, make ∠RPS = 80°. Let them intersect at S.

5. PQRS is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral PQRS = 1/2 × d × ( h₁ + h₂ ) sq. units

= 1/2 × 6.4 × (4.7 + 3.8)

= 3.2 × 8.5 = 27.2 cm²

Think

Is it possible to construct a quadrilateral PQRS with PQ = 5 cm, QR = 3 cm, RS = 6 cm, PS = 7 cm and PR = 10 cm. If not, why?

Solution:

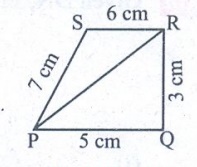
The lower triangle cannot be constructed as the sum of two sides

5 + 3 = 8 < 10 cm. So this quadrilateral cannot be constructed.