Angle Bisectors of a Triangle

Angle Bisectors of a Triangle

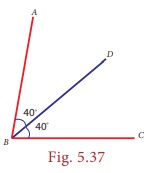
We have learnt about angle bisectors in the previous class. An angle bisector is a line or ray that divides an angle into two congruent angles. In the figure, ∠ABC is bisected by the line BD such that ∠ABD = ∠CBD.

Consider a triangle ABC. How many angles does a triangle have ? 3 angles. For each angle you can have an angle bisector as follows:

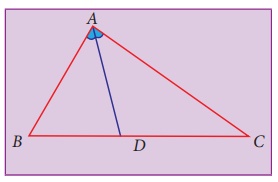
AD bisects ∠A into two congruent angles. Hence it is an angle bisector of ∠A.

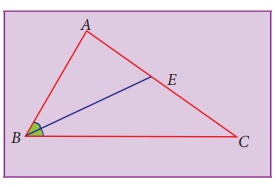
BE bisects ∠B into two congruent angles. Hence it is an angle bisector of ∠B.

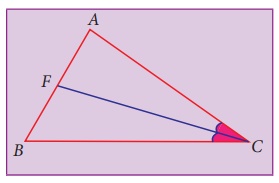
CF bisects ∠C into two congruent angles. Hence it is an angle bisector of ∠C.

Activity

1. Consider a paper cut-out of a triangle. Name it, say ABC.

2. Fold the triangle so that the opposite sides meet and contain the vertex. Repeat the same to find angle bisectors of other two angles also.

3. Trace all of the folds.

Do the angle bisectors pass through the same point?

Now you can repeat this activity for an obtuse-angled triangle and a right angled triangle. What is the conclusion? Do the angle bisectors pass through the same point in all the cases? Yes, we see that,

The three angle bisectors of any triangle are concurrent.

1. Incentre

The point of concurrence of the three angle bisectors of a triangle is called as its incentre, denoted by the letter I.

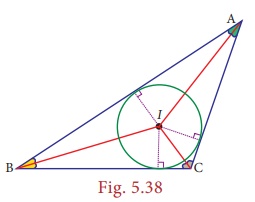
Why should it be called so? Because one can draw a circle inside of the triangle so that it touches all three sides internally, with centre at the point of concurrence of the angle bisectors. The lengths of a perpendicular line drawn from B incentre to each side is found to be same. Thus, the incentre is equidistant from the sides of the triangle.

Example 5.20

Identify the incentre of the triangle PQR.

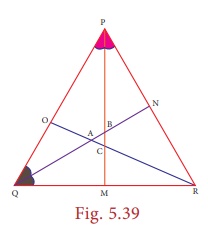
Solution:

Incentre is the point of intersection of angle bisectors.

Here, PM and QN are angle bisectors of ∠P and ∠Q respectively, intersecting at B.

So, the incentre of the triangle PQR is B.

(Can A and C be the incentre of ∆PQR? Why?)

The position of the Centroid, Orthocentre, Circumcentre and Incentre differs depending on the type of triangles given. The following points will help us in locating and remembering these.

(i) For all types of triangles, Centroid (G) and Incentre (I) will be inside the triangle.

(ii) The Orthocentre (H) will be inside in an acute angled triangle, outside in an obtuse angled triangle and on the vertex containing 90° in a right angled triangle.

(iii) The Circumcentre (S) will be inside in an acute angled triangle, outside in an obtuse angled triangle and on the hypotenuse in a right-angled triangle.

Try these

Identify the type of segment required in each  triangle:

(median, altitude, perpendicular bisector, angle bisector)

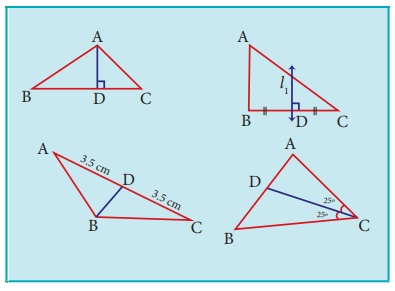
(i) AD = Altitude (ii) l₁ = Perpendicular bisector

(iii) BD = Median (iv) CD = Angular bisector

Activity

1. By paper folding, find the centroid, orthocentre, circumcentre and incentre of an equilateral triangle. Do they coinside?

2. By paper folding, find the centroid (G), orthocentre(H), circumcentre (S) and incentre (I) of a triangle. Join G,H,S and I. Are they collinear?