Perpendicular Bisectors of a Triangle

Perpendicular Bisectors of a Triangle

Let us first recall the following ideas.

Consider a triangle ABC. It has three sides. For each side you can have a perpendicular bisector as follows:

Surprisingly, all the three perpendicular bisectors of the sides of a triangle are concurrent at a point!

Activity

One can visualize the point of concurrence of the perpendicular bisectors, through simple paper folding. Try and see that,

The perpendicular bisectors of the sides of any triangle are concurrent.

As done in the earlier activity on Centroid, you can repeat the experiment for various types of triangle, acute, obtuse, right, isosceles and equilateral. Do you find anything special with the equilateral triangle in this case?

1. Circumcentre

The point of concurrence of the three perpendicular bisectors of a triangle is called as its Circumcentre, denoted by the letter S.

Why should it be called so? Because one can draw a circle exactly passing through the three vertices of the triangle, with centre at the point of concurrence of the perpendicular bisectors of sides. Thus, the circumcentre is equidistant from the vertices of the triangle.

Activity

Check if the following are true by paper-folding:

• The circumcentre of an acute angled triangle lies in the interior of the triangle.

• The circumcentre of an obtuse angled triangle lies in the exterior of the triangle.

• The circumcentre of a right triangle lies at the midpoint of its hypotenuse.

Example 5.19

In ∆ABC, S is the circumcentre, BC = 72 cm and DS = 15 cm. Find the radius of its circumcircle.

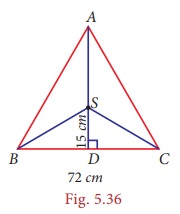
Solution:

As S is the circumcentre of ∆ABC, it is equidistant from A,B and C. So AS=BS=CS=radius of its circumcircle. As AD is the perpendicular bisector of BC, BD = 1/2 ×BC = 1/2 ×72 = 36 cm

In right angled triangle BDS, by Pythagoras theorem,

BS² = BD² +SD² = 36² + 15² = 1521 = 39²

⇒ BS = 39cm.

∴The radius of the circumcircle of ΔABC is 39 cm.