Converse of Pythagoras Theorem

Converse of Pythagoras Theorem

If in a triangle, the square on the greatest side is equal to the sum of squares on the other two sides, then the triangle is right angled triangle.

Example:

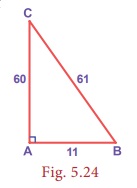
In the triangle ABC,

AB² + AC² = 11² + 60² = 3721 = 61² = BC²

Hence, ∆ABC is a right angled triangle.

(i) There are special sets of numbers a, b and c that makes the Pythagorean relationship true and these sets of special numbers are called Pythagorean triplets. Example: (3, 4, 5) is a Pythagorean triplet.

(ii) Let k be any positive integer greater than 1 and (a, b, c) be a Pythagorean triplet, then (ka, kb, kc) is also a Pythagorean triplet.

Examples:

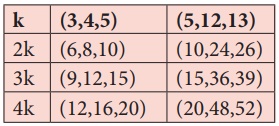
So, it is clear that we can have infinitely many Pythagorean triplets just by multiplying any Pythagorean triplet by k.

We shall now see a few examples on the use of Pythagoras theorem in problems.

Example 5.11

In the figure, AB ⊥ AC

a) What type of ∅ is ABC?

b) What are AB and AC of the ∆ABC ?

c) What is CB called as ?

d) If AC = AB then, what is the measure of ∠ B and ∠C ?

Solution:

a) ∆ABC is right angled as AB ⊥ AC at A.

b) AB and AC are legs of ∆ ABC .

c) CB is called as the hypotenuse.

d) ∠ B + ∠ C = 90º and equal angles are opposite to equal sides. Hence, ∠ B = ∠ C =90º /2 =45º

Example 5.12

Can a right triangle have sides that measure 5cm, 12cm and 13cm?

Solution:

Take a = 5 , b = 12 and c = 13

Now, a ² + b² = 5² + 12² = 25 + 144 = 169 = 13² = c²

By the converse of Pythagoras theorem, the triangle with given measures is a right angled triangle.

Example 5.13

A 20-feet ladder leans against a wall at height of 16 feet from the ground. How far is the base of the ladder from the wall?

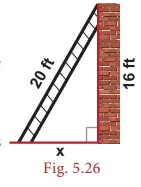
Solution:

The ladder, wall and the ground form a right triangle with the ladder as the hypotenuse. From the figure, by Pythagoras theorem,

20² = 16² + x²

⇒ 400 = 256 + x²

⇒ x² = 400 − 256 = 144 = 12²

⇒ x =12 feet

Therefore, the base (foot) of the ladder is 12 feet away from the wall.

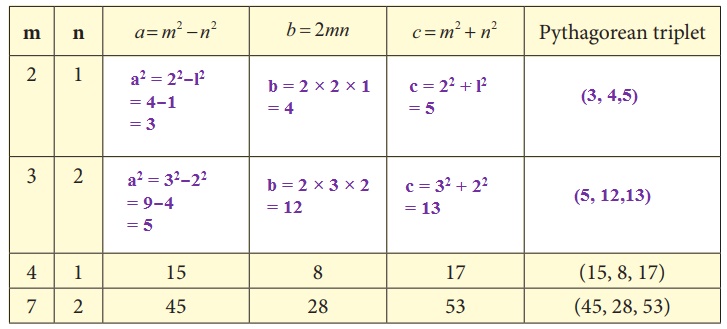
Activity

1. We can construct sets of Pythagorean triplets as follows.

Let m and n be any two positive integers (m > n):

(a, b, c) is a Pythagorean triplet if a = m² − n² , b = 2mn and c = m² + n² (Think, why?)

Complete the table.

2. Find all integer-sided right angled triangles with hypotenuse 85.

Solution:

(x + y)² − 2xy = 85²

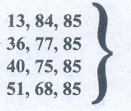 Pythagorean triplets with hypotenuse 85.

13, 84, 85

36, 77, 85

40, 75, 85

51, 68, 85

Example 5.14

Find LM, MN, LN and also the area of ∆ LON_.

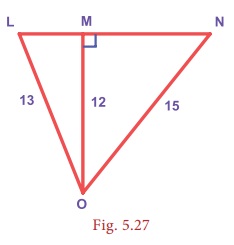
Solution:

From ∆LMO, by Pythagoras theorem,

LM² = OL² − OM²

⇒ LM² =13² −12² =169 −144 = 25 = 5²

∴ LM = 5 units

From ∆NMO, by Pythagoras theorem,

MN² = ON² − OM²

= 15² −12² = 225 −144 = 81= 9²

∴ MN = 9 units

Hence, LN = LM + MN = 5 + 9 = 14 units

Area of ∆LON = 1/2 × base × height

= 1/2 × LN × OM

= 1/2 × 14 × 12 = 84 square units.

Example 5.15

∆ABC is equilateral and CD of the right triangle BCD is 8 cm.

Find the side of the equilateral ∆ABC and also BD.

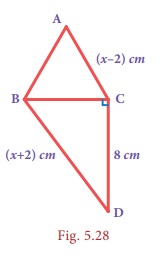
Solution:

As ∆ABC is equilateral from the figure, AB=BC=AC= (x−2) cm.

From ∆BCD, by Pythagoras theorem

BD² = BC² + CD²

⇒ ( x + 2)² = ( x − 2)² + 8²

 x² + 4x + 4 = x² − 4x + 4 + 8²

⇒ 8 x = 8²

⇒ x = 8cm

The side of the equilateral ∆ ABC = 6 cm and BD =10 cm.