Geometry | Chapter 5 | 8th Maths - Congruent Triangles | 8th Maths : Chapter 5 : Geometry
Chapter: 8th Maths : Chapter 5 : Geometry
Congruent Triangles
Congruent
Triangles
Consider
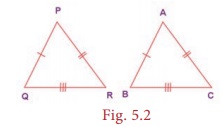
two given triangles PQR and ABC. They are said to be congruent (≡) if their corresponding
parts are congruent. That is PQ=AB, QR=BC and PR=AC and also ∠P = ∠A, ∠Q = ∠B and ∠R = ∠C. This is denoted as ∆PQR ≡ ∆ABC .
There are
4 ways by which one can prove that two triangles are congruent.
(i) SSS (Side – Side –
Side) Congruence
If the three
sides of a triangle are congruent to the three sides of another triangle, then the
triangles are congruent.
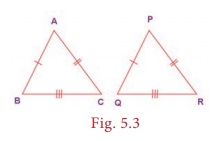
That is AB = PQ,
BC = QR and AC = PR
⇒
∆ABC ≡ ∆PQR.
(ii) SAS (Side – Angle
– Side) Congruence
If two sides
and the included angle (the angle between them) of a triangle are congruent to two
sides and the included angle of another triangle, then the triangles are congruent.
Here, AC = PQ, ∠A =
∠P and AB = PR and hence ∆ACB
≡ ∆PQR.

(iii) ASA (Angle-Side-Angle)
Congruence
If two angles
and the included side of a triangle are congruent to two angles and the included
side of another triangle, then the triangles are congruent. Here, ∠A = ∠R, CA=PR and ∠C = ∠P and hence ∆ABC ≡
∆RQP
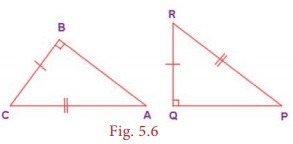
(iv) RHS (Right Angle –
Hypotenuse – Side) Congruence
If the hypotenuse
and a leg of one right triangle are congruent to the hypotenuse and a leg of another
right triangle, then the triangles are congruent. Here,
∠B = ∠Q =
90°, BC = QR and AC =
PR
(right angle)
(leg) (hypotenuse)
and hence
∆ABC ≡ ∆PQR.
Note
• Any segment or angle is congruent to itself! This is called Reflexive
property
• If two triangles are congruent, then their corresponding parts
are congruent. This is called CPCTC (Corresponding
parts of Congruent Triangles are Congruent).
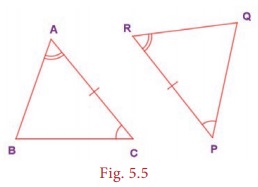
• If angles then sides
means if two angles are
equal in a triangle, then the sides opposite
to them are equal.
• If sides then angles
means if two sides are
equal in a triangle, then the angles opposite
to them are equal.
Try these
Match the following by their congruence property
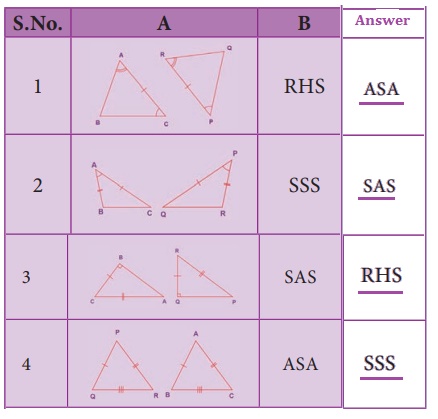
Answer: 1. (iv), 2.
(iii), 3. (i), 4. (ii)
Example 5.1
Find the
unknowns in the following figures
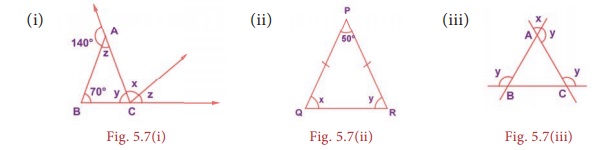
Solution:
(i) Now,
from Fig. 5.7 (i), 140º + ∠z =
180º (linear
pair)
⇒ ∠z =
180º - 140º = 40º
Also ∠x +
∠z =
70º + ∠z (exterior angle property)
⇒ ∠x = 70º
Also ∠z + ∠y + 70º = 180º (angle sum property
in ΔABC)
⇒ 40º
+ ∠y + 70º = 180º
⇒ ∠y = 180º - 110º = 70º
(ii) Now,
from Fig. 5.7(ii), PQ = PR
⇒ ∠Q = ∠R (angles
opposite to equal sides are equal)
⇒ ∠x = ∠y
⇒ ∠x+ ∠y + 50º = 180º (angle sum property in ΔPQR)
⇒ ∠2 x = 130º
⇒ ∠x = 65º
⇒ ∠y = 65º
(iii) Now,
from Fig. 5.7(iii), in ΔABC
∠A
= x (vertically
opposite angles)
Similarly
∠B = ∠C = x (Why?)
⇒ ∠A + ∠B + ∠C = 180º (angle
sum property in ΔABC)
⇒
3 x =180º
⇒ x = 60º
⇒ y = 180º − 60º = 120º
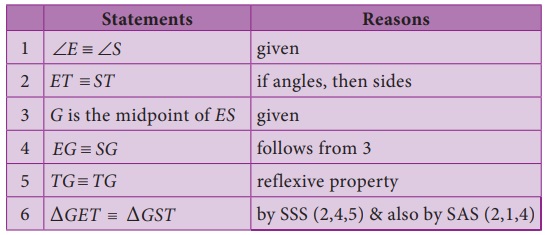
Example 5.2 (Illustrating SSS and SAS Congruence)
If ∠E = ∠S and G is the midpoint of ES, prove
that ∆GET ≡
∆GST.

Proof:
Think
In the figure, DA = DC and BA = BC.
Are the triangles DBA and DBC congruent? Why?
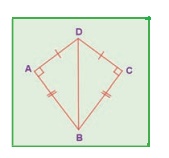
Solution:
Here AD = CD
AB = CB
DB = DB (common)
ΔDBA = ΔDBC [∵ By SSS congruency]
Also RHS rule also bind here to say their congruency.
Example 5.3 (Illustrating ASA Congruence)
If ∠YTB ≡
∠YBT and ∠BOY ≡
∠TRY , prove that ∆BOY ≡ ∆TRY
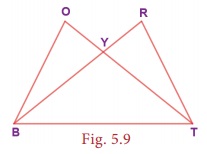
Proof:
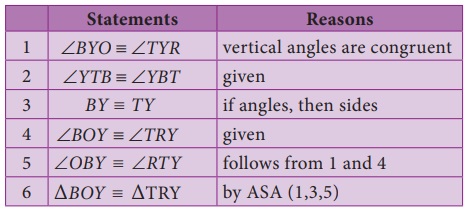
Example 5.4 (Illustrating RHS Congruence)
If TAP is an isosceles triangle with TA = TP
and ∠TSA
= 90°.
(i) Is ∆TAS ≡ ∆TPS ? Why?
(ii) Is ∠P = ∠A? Why?
(iii) Is
AS = PS? Why?
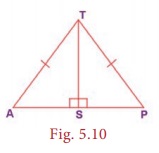
Proof:
(i) TA =
TP (hypotenuse) and ∠TSA = 90
TS is common
(leg)
Hence, by
RHS congruence, ∆TAS ≡
∆TPS
(ii) Given
TA = TP
∠P = ∠A (if angles then sides)
(iii) From
(i) ∆TAS ≡
∆TPS ,
By CPCTC
AS=PS
SSA and ASS properties are not sufficient to prove that two
triangles are congruent. This is explained in the given figure. By construction,
in triangles ABD and ABC, BC = BD = a. Also, AB and ∠BAZ are common. But AC ≠ AD. So, ∆ABD is not congruent to ∆ABC and so SSA fails.
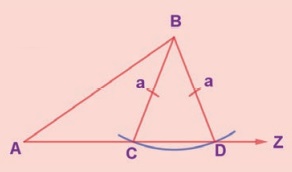
Related Topics