Exercise 5.1 (Congruent and Similar Triangles)

Exercise 5.1

1. Fill in the blanks with the correct term from the given list.

(in proportion, similar, corresponding, congruent, shape, area, equal)

(i) Corresponding sides of similar triangles are _______. [Answer: in proportion]

(ii) Similar triangles have the same _________ but not necessarily the same size. [Answer: shape]

(iii) In any triangle ______ sides are opposite to equal angles. [Answer: equal]

(iv) The symbol ≡ is used to represent _______ triangles. [Answer: congruent]

(v) The symbol ~ is used to represent ________ triangles. [Answer: similar]

2. In the given figure, ∠CIP ≡ ∠COP and ∠HIP ≡ ∠HOP . Prove that IP ≡ OP.

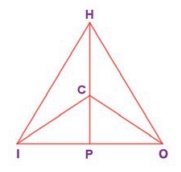
Solution:

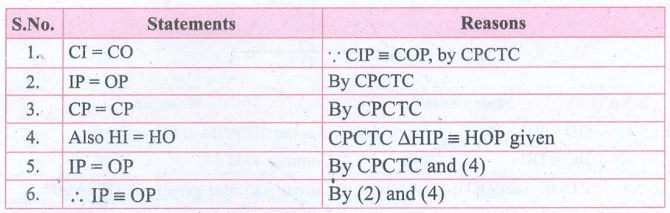
Statements : Reasons

1. CI = CO  : ∵ CIP ≡ COP, by CPCTC

2. IP = OP :  By CPCTC

3. CP = CP : By CPCTC

4. Also HI = HO : CPCTC ΔHIP ≡ HOP given

5. IP = OP : By CPCTC and (4)

6. ∴ IP ≡ OP : By (2) and (4)

3. In the given figure, AC ≡ AD and ∠CBD ≡ ∠DEC . Prove that ∆ BCF ≡ ∆EDF .

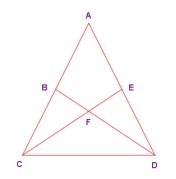
Solution:

Statements : Reasons

1. ∠BFC = ∠EFD : vertically opposite angles

2. ∠CBD = ∠DEC : Angles on the same base given

3. ∠BCF = ∠EDF : Remaining angles of ΔBCF and ΔEDF

4. ΔBCF ≡ ΔEDF : By (1) and (2) AAA criteria

4. In the given figure, ∆ BCD is isosceles with base BD and ∠BAE ≡ ∠DEA . Prove that AB ≡ ED .

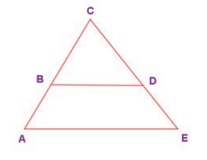
Solution:

Statements : Reasons

1. ∠BAE ≡ ∠DEA : Given

2. AC = EC : By (1) sides opposite to equal angles are equal

3. BC = DC : Given BCD is isosceles with base BD

4. AC − BC = EC − DC : 2 − 3

5. AB ≡ ED : By 4

5. In the given figure, D is the midpoint of OE and ∠CDE = 90°. Prove that ∆ODC ≡ ∆EDC

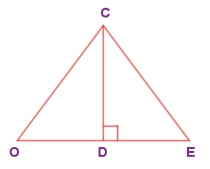
Solution:

Statements : Reasons

1. OD = ED : D is the midpoint of OE (given)

2. DC = DC : Common side

3. ∠CDE = ∠CDO = 90° : Linear pair and given ∠CDE = 90°

4. ΔODC ≡ ΔEDC : By RHS criteria

6. Is PRQ ≡ QSP ? Why?

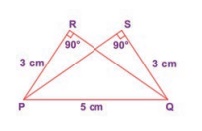
Solution:

In ΔPRQ and ΔPSQ

∠PRQ = ∠PSQ = 90° given

PR = QS = 3 cm given

PQ = PQ = 5 cm common

It satisfies RHS criteria

∴  ΔPRQ congruent to ΔQSP.

7. From the given figure, prove that ∆ABC ~ ∆EDF

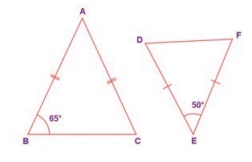
Solution:

From the ΔABC, AB = AC

It is an isosceles triangle

Angles opposite to equal sides are equal

∴ ∠B = ∠C = 65°

∴ ∠B + ∠C = 65° + 65°

= 130°

We know that sum of three angles is a triangle = 180°

∠A + ∠B + ∠C = 180°

∠A + 130° = 180°

∠A = 180° − 130°

∠A = 50°

From ΔEDF, ∠E = 50°

∴  Sum of Remaining angles = 180° − 50° = 130°

DE = FD

∴ ∠D = ∠F

From ΔABC and ΔEDF ∴

∠D = 130/2 = 65°

∠A = ∠E = 50°

∠B = ∠D = 65°

∠C = ∠F = 65°

∴ By AAA criteria ΔEDF ≈ ΔABC

8.  In the given figure YH || TE . Prove that ∆WHY ~ ∆WET and also find HE and TE.

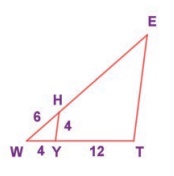
Solution:

Statements : Reasons

1. ∠EWT = ∠HWY : Common Angle

2. ∠ETW = ∠HYW : Since YH ‖‖ TE, corresponding angles

3. ∠WET = ∠WHY : Since YH ‖‖ TE corresponding angles

4. ΔWHY∼ ΔWET : By AAA criteria

Also ΔWHY ~ ΔWET

∴  Corresponding sides are proportionated

WH / WE = HY / TE = WY / WT

6 / [ 6 + HE ] = 4/TE = 4/16

6 / [6 + HE] = 4/16

6 + HE = [6/4] × 16

6 + HE = 24

∴  HE = 24 −  6

HE = 18

Again 4/TE = 4/16

ET = 4/4

TE = 16

9. In the given figure, if ∆EAT ~ ∆BUN , find the measure of all angles.

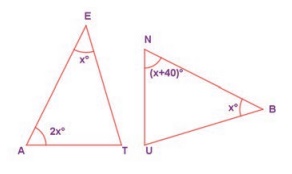
Solution:

Given ΔEAT ≡ ΔBUN

∴  Corresponding angles are equal

∴  ∠E =  ∠B  ...(1)

∠A =  ∠U

∠T =  ∠N

∠E = x°

∠A = 2x°

Sum of three angles of a triangle = 180°

In ΔEAT, x + 2x +  ∠T = 180°

∠T = 180° − (x° + 2x°) 

∠T = 180° − 3x° ……..(4)

Also in ΔBUN

(x + 40)° + x° + ∠U = 180°

x + 40° + x + ∠U = 180°

2x° + 40° + ∠U = 180°

∠U = 180° − 2x − 40° = 140°− 2x°

Now by (2)

∠A = ∠U

2x = 140° − 2x°

2x + 2x = 140°

4x = 140°

x = 140°/4 = 35°

∠A = 2x° = 2 × 35° = 70°

∠N = x + 40° = 35° + 40° = 75°

∴  ∠T = ∠N = 75°

∠E = ∠B = 35°

∠A = ∠U = 70°

10. In the given figure, UB ||AT and CU ≡ CB Prove that ∆CUB ~ ∆CAT and hence ∆CAT is isosceles.

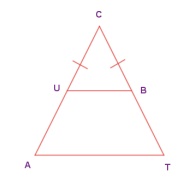
Solution:

Statements: Reasons

1. ∠CUB = ∠CBU : ∵  In ΔCUB, CU = CB

2. ∠CUB = ∠CAB : ∵  UB || AT, corresponding angle if CA is the transversal.

3. ∠CBU = ∠CTA : CT is transversal UB || AT, corresponding angle common angle.

4. ∠UCB=  ∠ACT : common angle

5. ΔCUB ∼ ΔCAT : By AAA criteria

6. CA = CT : ∵  ∠CAT = ∠CTA

 7. Also ΔCAT is isosceles : By 1, 2 and 3 and sides opposite to equal angles are equal.

Objective Type Questions

11. Two similar triangles will always have ________angles

(A) acute

(B) obtuse

(C) right

(D) matching

[Answer: (D) matching]

12. If in triangles PQR and XYZ, PQ/ XY = QR/YZ then they will be similar if

 (A) ∠Q = ∠Y

(B) ∠P = ∠Y

(C) ∠Q = ∠X

(D) ∠P = ∠Z

[Answer: (a) ∠Q = ∠Y]

13. A flag pole 15 m high casts a shadow of 3 m at 10 a.m. The shadow cast by a building at the same time is 18.6 m. The height of the building is

(A) 90 m

(B) 91 m

(C) 92 m

(D) 93 m

[Answer: (D) 93 m]

14. If ∆ABC ~ ∆PQR in which ∠A = 53º and ∠Q = 77º , then ∠R is

(A) 50°

(B) 60°

(C) 70°

(D) 80°

[Answer: (A) 50°]

15. In the figure, which of the following statements is true?

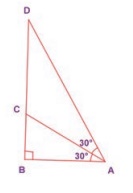
(A) AB = BD

(B) BD < CD

(C) AC = CD

(D) BC = CD

[Answer: (C) AC = CD]

Answer:

Exercise 5.1

1. (i) in proportion (ii) shape (iii) equal (iv) congruent (v) similar

6. Yes, RHS Congruence

8. HE =18,TE =16

9. ∠T = ∠N = 75º,∠E = ∠B = 35º,∠A = ∠U = 70º

11. (D) matching

12.(A) ∠Q = ∠Y 

13. (D) 93 m 

14. (A) 50º

15. (C) AC = CD