Exercise 5.4 (Construction of Quadrilaterals and Trapeziums)

Exercise 5.4

I. Construct the following quadrilaterals with the given measurements and also find their area.

1. ABCD, AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm and AC= 6.2 cm.

Solution:

Given :

AB = 5 cm, BC = 4.5 cm, CD = 3.8 cm, DA = 4.4 cm, AC= 6.2 cm

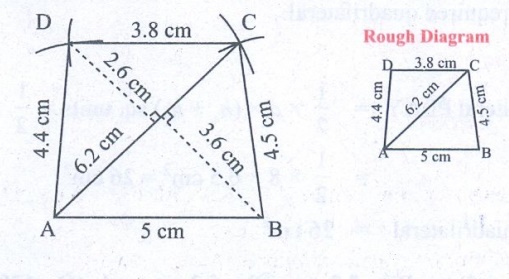
Steps:

1. Draw a line segment AB = 5 cm

2. With A and B as centers drawn arcs of radii 6.2 cm and 4.5cm respectively and let them cut at C.

3. Joined AC and BC.

4. With A and C as centrers drawn arcs of radii 4.4cm and 3.8 cm respectively and let them at D.

5. Joined AD and CD.

6. ABCD is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral ABCD 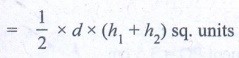 = 1/2 × d × (h₁ + h₂) sq. units

= 1/2 × 6.2 × (2.6 + 3.6) cm² = 3.1 × 6.2 = 19.22 cm² 

2. PLAY, PL= 7 cm, LA = 6 cm, AY= 6 cm, PA = 8 cm and LY = 7 cm.

Solution:

Given 

PL = 7 cm, LA = 6 cm, AY= 6 cm, PA = 8 cm, LY = 7 cm

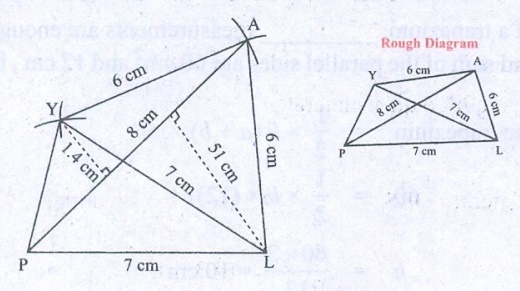
Steps:

1. Drawn a line segment PL = 7 cm

2. With P and L as centers, drawn arcs of radii 8 cm and 6 cm respectively, let them cut at A.

3. Joined PA and LA.

4. With L and A as centers, drawn arcs of radii 7 cm and 6 cm respectively and let them cut at Y.

5. Joined LY, PY and AY.

6. PLAY is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral PLAY 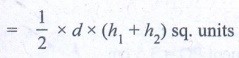= 1/2 × d × (h₁ + h₂) sq. units = 1/2 × 8 × (5.1 + 1.4) cm²

= 1/2  × 8 × 6.5 cm² = 26 cm²

Area of the quadrilateral = 26 cm²

3. PQRS, PQ=QR= 3.5 cm, RS= 5.2 cm, SP = 5.3 cm and ∠Q = 120°.

Solution:

Given: 

PQ = QR − 3.5 cm, RS = 5.2 cm, SP = 5.3 cm , ∠Q =120°

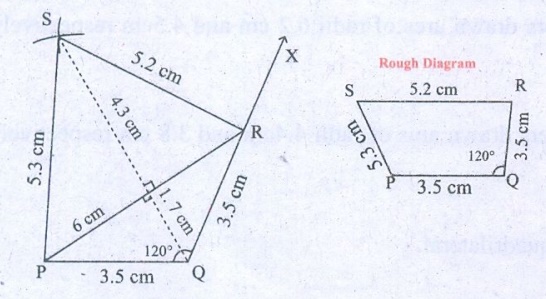
Steps:

1. Draw a line segment PQ = 3.5 cm

2. Made ∠Q = 120°. Drawn the ray QX. 

3. With Q as centre drawn an arc of radius 3.5 cm. Let it cut the ray QX at R.

4. With R and P as centres drawn arcs of radii 5.2 cm respectively and let them cut at S.

5. Joined PS and RS.

6. PQRS is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral PQRS 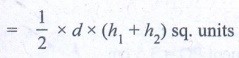 = 1/2 × d × (h₁ + h₂) sq. units

= 1/2 × 6 × (4.3 + 1.7) cm²

= 3 × 6 cm²

= 18 cm²

Area of the quadrilateral PQRS = 18 cm²

4. MIND, MI =3.6 cm, ND = 4 cm, MD= 4 cm, ∠M = 50° and ∠D = 100°.

Solution:

Given:

 mi = 3.6 cm, ND = 4 cm, MD = 4 cm,  ∠M = 50° and ∠D = 100°

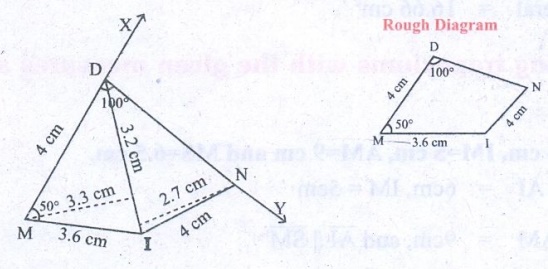
Steps:

1. Drawn a line segment MI = 3.6 cm

2. At M on MI made an angle ∠IMX = 50°

3. Drawn an arc with center M and radius 4 cm let it cut MX it D

4. At D on DM made an angle ∠MDY = 100°

5. With I as center drawn an arc of radius 4 cm, let it cut DY at N.

6. Joined DN and IN.

7. MIND is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral MIND 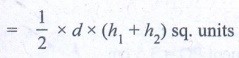 = 1/2 × d × (h₁ + h₂) sq. units = 1/2 × 3.2 × (2.7 + 3.3) cm²

= 1/2 × 3.2 × 6 cm² = 9.6 cm²

Area of the quadrilateral = 9.6 cm²

5. AGRI, AG= 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.

Solution:

AG = 4.5 cm, GR = 3.8 cm, ∠A = 90°, ∠G = 110°, ∠R = 90°

Steps:

1. Draw a line segment AG = 4.5 cm

2. At G on AG made ∠AGX =110°

3. With G as centre drawn an arc of radius 3.8 cm let it cut GX at R.

4. At R on GR made ∠GRZ = 90°

5. At A on AG made ∠GAY = 60°

6. AY and RZ meet at I.

7. AGRI is the required quadrilateral.

Calculation of Area:

Area of the quadrilateral AGRI 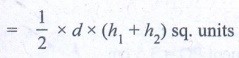 = 1/2 × d × (h₁ + h₂) sq. units = 1/2 × 6.8 × (2.5 + 2.4) cm²

= 1/2 × 6.8 × 4.9 cm² = 3.4 × 4.9 cm²

Area of the quadrilateral = 16.66 cm²

II. Construct the following trapeziums with the given measures and also find their area.

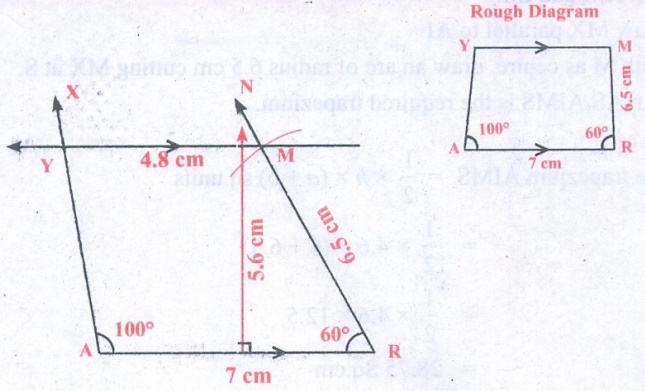
1. AIMS with ̅A̅I̅ || S̅M̅, AI = 6 cm, IM = 5 cm, AM = 9 cm and MS = 6.5 cm.

Solution:

Given AI = 6cm, IM = 5cm

AM = 9cm, and A̅I̅ || S̅M̅ 

MS = 6.5 cm

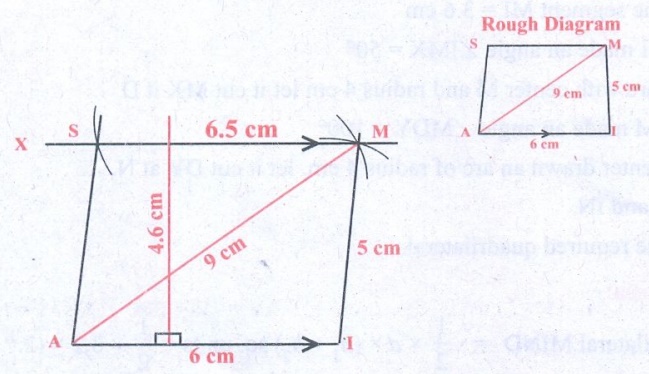
Construction :

Steps:

1. Draw a line segment AI = 6cm.

2. With A and I as centres, draw arcs of radii 9 cm and 5 cm respectively and let them cut at M

3. Join AM and IM.

4. Draw MX parallel to AI

5. With M as centre, draw an arc of radius 6.5 cm cutting MX at S.

6. Join AS AIMS is the required trapezium.

Calculation of Area:

Area of the trapezium AIMS 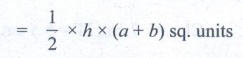 = 1/2 × h × (a + b) sq.units

= 1/2 × 4.6 × (6 + 6.5)

= 1/2 × 4.6 × 12.5

= 28.75 Sq.cm

2. CUTE with C ̅U || ̅E̅T̅, CU = 7 cm, ∠UCE = 80°, CE = 6 cm and TE = 5 cm.

Solution:

Given : In the trapezium CUTE,

CU = 7cm, ∠UCE = 80°,

CE = 6 cm, TE = 5cm and C̅U̅ || E̅T̅ 

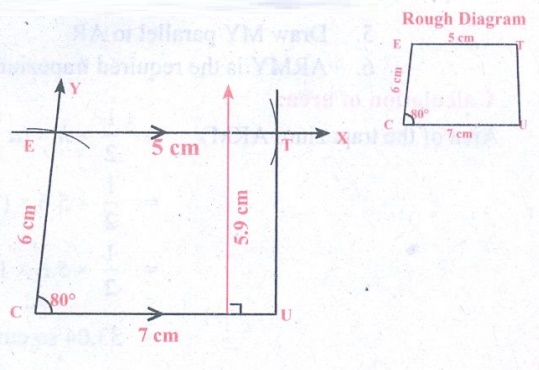
Construction:

Steps:

1. Draw a line segment CU = 7 cm.

2. Construct an angle ∠UCE = 80° at C

3. With C as centre, draw an arc 5 of radius 6 cm cutting CY at E

4. Draw EX parallel to CU

5. With E as centre, draw an arc of radius 5 cm cutting EX at T

6. Join UT. CUTE is the required trapezium.

Calculation of area:

Area of the trapezium CUTE 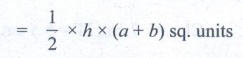 = 1/2 × h × (a + b) sq.units

= 1/2 × 5.9 × (7 + 5) sq.units

= 35.4 sq.cm

3. ARMY with A ̅R || Y ̅M, AR = 7 cm, RM = 6.5 cm ∠RAY = 100° and ∠ARM = 60°

Solution:

Given :

In the trapezium ARMY

AR = 7 cm, RM = 6.5 cm,

∠RAY = 100° and ARM = 60°, A̅R̅ || Y̅M̅

Construction:

Steps:

1. Draw a line segment AR = 7 cm.

2. Construct an angle ∠RAX = 100° at A

3. Construct an angle ∠ARN = 60° at R

4. With R as centre, draw an arc of radius 6.5 cm cutting RN at M

5. Draw MY parallel to AR

6. ARMY is the required trapezium.

Calculation of area:

Area of the trapezium ARMY 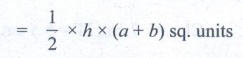= 1/2 × h × (a + b) sq.units

= 1/2 × 5.6 × (7 + 4.8) sq.units

= 1/2 × 5.6 × 11.8

= 33.04 sq.cm

4. CITY with C ̅I || Y̅̅T, CI = 7 cm, IT = 5.5 cm, TY = 4 cm and YC = 6 cm.

Solution:

Given :

In the trapezium CITY,

CI = 7 cm, IT = 5.5 cm, TY = 4 cm

YC = 6 cm, and C̅I̅ || Y̅T̅ 

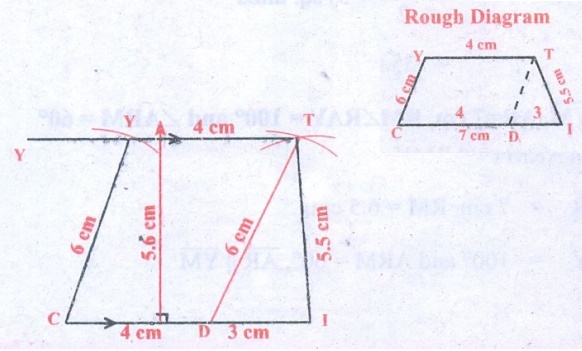
Construction:

Steps:

1. Draw a line segment CI = 7 cm.

2. Mark a point D on CI such that CD = 4 cm

3. With D and I as centres, draw arcs of radii 6 cm and 5.5 cm respectively. Let them cut at T. join DT and IT.

4. With C as centre, draw an arc of radius 6 cm

5. Draw TY parallel to CI. Let the  line cut the previous arc at Y.

6. Join CY. CITY is the required trapezium.

Calculation of area:

Area of the trapezium CITY 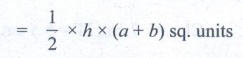 = 1/2 × h × (a + b) sq.units

= 1/2 × 5.5 × (7 + 4) sq.units

= 1/2 × 5.5 × 11

= 30.25 sq.cm