Properties of Mathematical expectation and variance

Properties of Mathematical expectation and variance

(i) E(aX + b) = aE( X ) + b , where a and b are constants

Proof

Let X be a discrete random variable

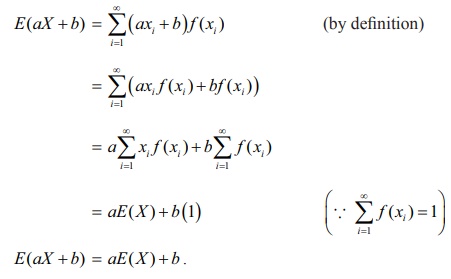
Similarly, when X is a continuous random variable, we can prove it, by replacing summation by integration.

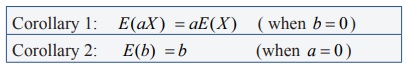
(ii) Var ( X ) = E ( X² ) −( E ( X ))²

Proof

We know

E ( x) = μ

Var ( X ) = E (X – μ)²

= E (X² – 2Xμ + μ²)

= E (X²) – 2μE(X) + μ²

(Since μ is a constant)

= E (X²) – 2μμ + μ² = E(X²) – μ²

Var ( X ) = E (X²) – (E (X))²

An alternative formula to compute variance of a random variable X is

 σ² = Var ( X ) = E( X²) – (E( X ))²

(iii) Var(aX +b) = a²Var (X ) where a and b are constants

Proof

Var ( aX + b) = E (( aX + b) – E ( aX + b))²

= E ( aX + b – aE( X ) – b))²

= E (aX – aE ( X )) ²

= E ( a ( X −E( X )))²

= a² E (X – E( X ))² .

Hence Var ( aX + b) = a²Var ( X )

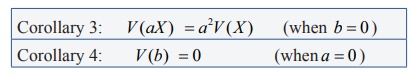
Variance gives information about the deviation of the values of the random variable about the mean μ. A smaller σ ² implies that the random values are more clustered about the mean, similarly, a bigger σ ² implies that the random values are more scattered from the mean.

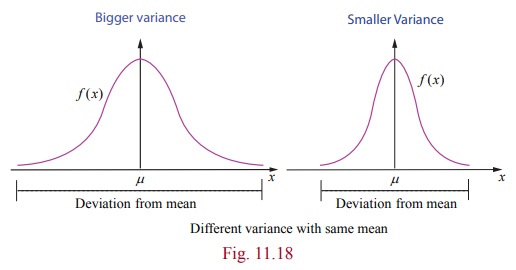
The above figure shows the pdfs of two continuous random variables whose curves are bell-shaped with same mean but different variances.

Example 11.16

Suppose that f ( x) given below represents a probability mass function,

Find (i) the value of c (ii) Mean and variance.

Solution

(i) Since f ( x) is a probability mass function, f (x) ≥ 0 for all x , and ∑_xf (x) = 1 .

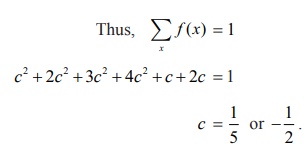
Since f (x) ≥ 0 for all x , the possible value of c is 1/5.

Hence, the probability mass function is

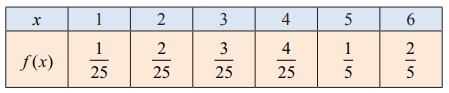
(ii) To find mean and variance, let us use the following table

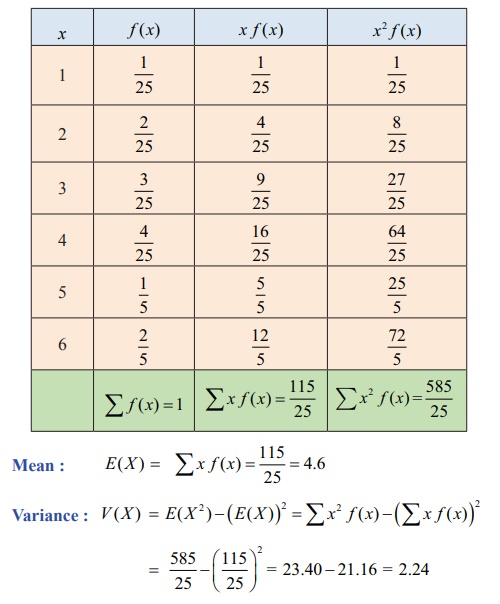
Therefore the mean and variance are 4.6 and 2.24 respectively.

Example 11.17

Two balls are chosen randomly from an urn containing 8 white and 4 black balls. Suppose that we win Rs 20 for each black ball selected and we lose Rs10 for each white ball selected. Find the expected winning amount and variance.

Solution

Let X denote the winning amount. The possible events of selection are (i) both balls are black, or (ii) one white and one black or (iii) both are white. Therefore x is a random variable that can be defined as

 X (both are black balls) = ₹ 2(20) = ₹ 40

 X (one black and one white ball) = ₹ 20 − ₹ 10 = ₹10

X (both are white balls) = ₹ (− 20) = − ₹ 20

Therefore X takes on the values 40,10 and −20

Total number of balls n = 12

Example 11.18

Find the mean and variance of a random variable X , whose probability density function is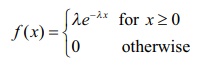 

Solution