Probability Mass Function

Probability Mass Function

The probability that a discrete random variable X takes on a particular value x, that is P ( X = x) , is frequently denoted by f ( x) or p ( x) . The function f ( x) is typically called the probability mass function, although some authors also refer to it as the probability function or the frequency function. In this chapter, when the random variable is discrete, the common terminology the probability mass function is used and its common abbreviation is pmf.

Definition 11.3 (Probability mass function)

If X is a discrete random variable with discrete values x1 , x2 , x3 , xn , then the function denoted by f (.) or p(.) and defined by

f ( xk ) = P ( X= xk ), for k =1, 2, 3, n,

is called the probability mass function of X

Theorem 11.1 (Without proof)

The function f ( x) is a probability mass function if and only if it satisfies the following properties for the set of real values x1, x2, x3, ... xn ....

(i) f (xk) ≥ 0 for k =1, 2, 3, n, and

(ii) ∑k f (xk) =1

Note:

(i) The set of probabilities { f (xk ) = P ( X = xk ), k = 1, 2, 3,. . . . n , . . . } is also known as probability distribution of discrete random variable

(ii) Since the random variable is a function, it can be presented

(a) in tabular form (b) in graphical form and (c) in an expression form

Example 11.5

Two fair coins are tossed simultaneously (equivalent to a fair coin is tossed twice). Find the probability mass function for number of heads occurred.

Solution

The sample space S = { H , T} × {H , T}

That is S = { TT , TH, HT , HH }

Let X be the random variable denoting the number of heads.

Therefore

X (TT) =0,

X (TH) =1,

X (HT) = 1, and

X (HH) =2.

Then the random variable X takes on the values 0, 1 and 2

The probabilities are given by

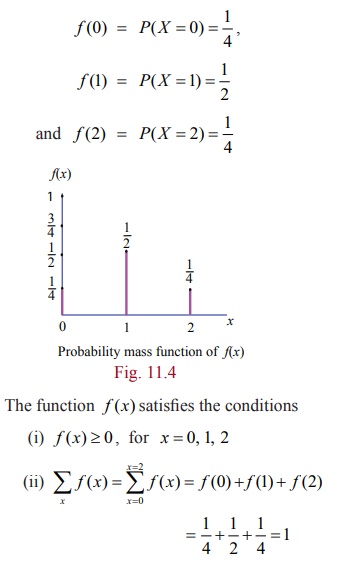
Therefore f ( x) is a probability mass function.

The probability mass function is given by

Example 11.6

A pair of fair dice is rolled once. Find the probability mass function to get the number of fours.

Solution

Let X be a random variable whose values x are the number of fours.

The sample space S is given in the table.

It can also be written as

S = {(i, j)} , where i = 1, 2, 3,. . .6 and j = 1, 2, 3, 6

Therefore X takes on the values of 0, 1, and 2.

We observe that

(i) X = 0, if (i , j) for i ≠ 4, j ≠ 4,

(ii) X = 1, if (1,4) , (2,4) , (3,4) , (5,4) , (6,4) , (4,1) , (4, 2) , (4, 3) , (4, 5) , (4, 6)

(iii) X = 2, if (4, 4) ,

Therefore,