Cumulative Distribution Function or Distribution Function

Cumulative Distribution Function or Distribution Function

There are many situations to compute the probability that the observed value of a random variable X will be less than or equal to some real number x . Writing F( x) = P (X≤ x) for every real number x , we call F ( x) , the cumulative distribution function or distribution function of the random variable X and its common abbreviation is cdf .

Definition 11.4: (cumulative distribution function)

The cumulative distribution function F ( x) of a discrete random variable X , taking the values x1 , x2 , x3 , such that x1 < x2 < x3 < … with probability mass function f (xi) is

F ( x) = P ( X ≤ x ) = ∑xi≤x f ( xi ), x ∈ ℝ

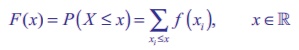
The distribution function of a discrete random variable is known as Discrete Distribution Function. Although, the probability mass function f ( x) is defined only for a set of discrete values x1, x2 , x3 , . . . , the cumulative distribution function F ( x) is defined for all real values of x ∈ ℝ.

We can compute the cumulative distribution function using the probability mass function

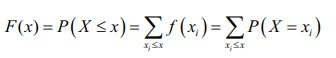
If X takes only a finite number of values x1 , x2 , x3 , . . . xn , where x1 < x2 < x3 <, . . .  < xn , then the cumulative distribution function is given by

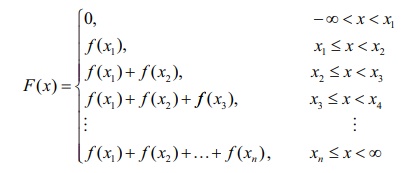
For a discrete random variable X, the cumulative distribution function satisfies the following properties.

(i) 0 ≤ F (x) ≤ 1 , for all x ∈ ℝ.

(ii) F ( x) is real valued non-decreasing function { x < y, then F ( x) ≤ F ( y) .

(iii) F ( x) is right continuous function (limx→a+ F(x) =  F (a) .

(iv) lim x → -∞ F (x) = F(-∞) = 0 .

(v) lim x → +∞ F (x) = F(+∞) = 1 .

(vi) P (x1 < X ≤  x2 ) = F (x2) − F (x1).

(vii) P (X > x) = 1 − P (X≤ x) = 1 − F (x) .

(viii) P ( X = xk ) = F( xk ) − F( xk− ) .

Note

Some authors use left continuity in the definition of a cumulative distribution function F ( x) , instead of right continuity.