Mathematical Expectation

Mathematical Expectation

One of the important characteristics of a random variable is its expectation. Synonyms for expectation are expected value, mean, and first moment.

The definition of mathematical expectation is driven by conventional idea of numerical average.

The numerical average of n numbers, say a₁ , a₂ , a₃ , , a_n is

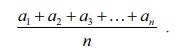
The average is used to summarize or characterize the entire collection of n numbers a₁ , a₂ , a₃ , . . . , a_n , with single value.

Illustration 11.7

Consider ten numbers 6, 2, 5, 5, 2, 6, 2, − 4, 1, 5 .

The average is [6 + 2 + 5 + 5 + 2 + 6 + 2 − 4 + 1 + 5]/10 = 3

If ten numbers 6, 2, 5, 5, 2, 6, 2, − 4, 1, 5 are considered as the values of a random variable X the probability mass function is given by

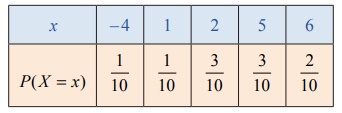
The above calculation for average can also be rewritten as

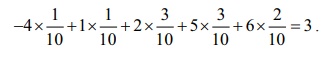
This illustration suggests that the mean or expected value of any random variable may be obtained by the sum of the product of each value of the random variable by its corresponding probability.

So average = ∑ (value of x ) × (probability)

This is true if the random variable is discrete. In the case of continuous random variable, the mathematical expectation is essentially the same with summations being replaced by integrals.

Two quantities are often used to summarize a probability distribution of a random variable X . In terms of statistics one is central tendency and the other is dispersion or variability of the probability distribution. The mean is a measure of the centre tendency of the probability distribution, and the variance is a measure of the dispersion, or variability in the distribution. But these two measures do not uniquely identify a probability distribution. That is, two different distributions can have the same mean and variance. Still, these measures are simple, and useful in the study of the probability distribution of X .

Mean

Definition 11.8 : (Mean)

Suppose X is a random variable with probability mass (or) density function f(x) . The expected value or mean or mathematical expectation of X , denoted by E( X ) or μ is

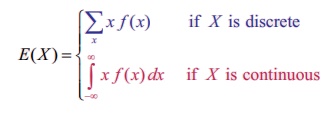
The expected value is in general not a typical value that the random variable can take on. It is often helpful to interpret the expected value of a random variable as the long-run average value of the variable over many independent repetitions of an experiment.

Theorem 11.3 (Without proof)

Suppose X is a random variable with probability mass (or) density function f (x) . The expected value of the function g(X) , a new random variable is

If g( X ) = x^k the above theorem yield the expected value called the k-th moment about the origin of the random variable X.

Therefore the k-th moment about the origin of the random variable X is

Note

When k = 0 , by definition,

Variance

Variance is a statistical measure that tells us how measured data vary from the average value of the set of data. Mathematically, variance is the mean of the squares of the deviations from the arithmetic mean of a data set. The terms variability, spread, and dispersion are synonyms, and refer to how spread out a distribution is.

Definition 11.9: (Variance)

The variance of a random variable X denoted by Var( X ) or V ( X ) or σ ² (or σ_x² ) is

 V (X ) = E(X − E(X ))² = E(X − μ)²

Square root of variance is called standard deviation. That is standard deviation √V( X ) . The variance and standard deviation of a random variable are always non negative.