Discrete random variables

Discrete random variables

In this section we discuss

(i) Discrete random variables

(ii) Probability mass function

(iii) Cumulative distribution function.

(iv) Obtaining cumulative distribution function from probability mass function.

(v) Obtaining probability mass function from cumulative distribution function.

If the range set of the random variables is discrete set of numbers then the inverse image of random variable is either finite or countably infinite. Such a random variable is called discrete random variable. A random variable defined on a discrete sample space is discrete.

Definition 11.2 (Discrete Random Variable)

A random variable X is defined on a sample space S into the real numbers is called discrete random variable if the range of X is countable, that is, it can assume only a finite or countably infinite number of values, where every value in the set S has positive probability with total one.

Remark

It is also possible to define a discrete random variable on continuous sample space. For instance,

(i) for a continuous sample space S = [0,1] , the random variable defined by X (ω) = 10 for all ω ∈ S, is a discrete random variable.

(ii) for a continuous sample space S = [0, 20] , the random variable defined by

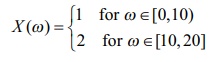
is a discrete random variable.