Probability Mass Function from Cumulative Distribution Function

Probability Mass Function from Cumulative Distribution Function

For a discrete random variable X, the cumulative distribution function F has jumps at each of the xi , and is constant between successive xi ′s . The height of the jump at xi f( xi ) ; in this way the is probability at xi can be retrieved from F .

Suppose X is a discrete random variable taking the values x1 , x2 , x3 , such that x1 < x2 , < x3 and F ( xi ) is the distribution function. Then the probability mass function f ( xi ) is given by

f (xi) = F (xi ) F (xi-1 ) , i = 1, 2, 3, . . .

Note

The jump of a function F ( x) at x = a is |F ( a + ) − F ( a − )|. Since F is non-decreasing and continuous to the right, the jump of a cumulative distribution function F is P( X = x) = F( x) − F( x− ) .

Here the jump (because of discontinuity) acts as a probability. That is, the set of discontinuities of a cumulative distribution function is at most countable!

Example 11.9

Find the probability mass function f ( x) of the discrete random variable X whose cumulative distribution function F ( x) is given by

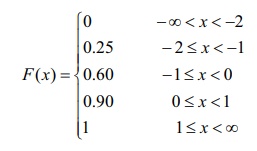
Also find (i) P( X < 0) and (ii) P( X ≥ − 1) .

Solution

Since X is a discrete random variable, from the given data, X takes on the values −2, −1, 0, and 1.

For discrete random variable X, by definition, we have f ( x) = P( X = x)

Therefore left hand limit of F(x) at x = −2 is F ( −2 − )

f(−2) = P(X = − 2) = F(− 2) −  F(− 2 −  ) = 0.25 − 0 = 0.25.

Similarly for other jump points, we have

f (−1) = P(X = − 1) = F(− 1) −  F(−2) = 0.60 − 0.25 = 0.35.

f (0) = P(X = 0) = F(0) −  F(−1) = 0.90 −  0.60 = 0.30 ,

f (1) = P( X = 1) = F(1) − F(0) = 1 −  0.90 = 0.10 .

Therefore the probability mass function is

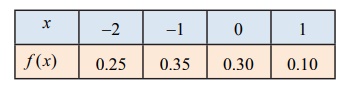
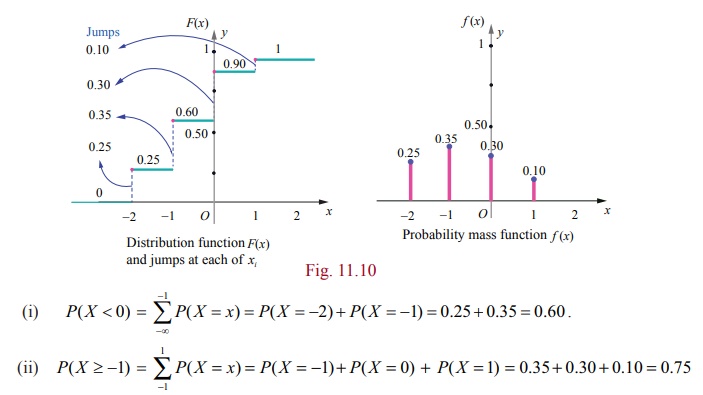
The distribution function F ( x) has jumps at x = − 2, − 1, 0, and 1. The jumps are respectively 0.25, 0.35, 0.30, and 0.1 is shown in the figure given below.

These jumps determine the probability mass function

Example 11.10

A random variable X has the following probability mass function.

Find (i) P (2 < X < 6) (ii) P (2 ≤ X < 5) (iii) P(X ≤ 4) (iv) P(3< X)

Solution

Since the given function is a probability mass function, the total probability is one. That is ∑x f (x) = 1.

From the given data k + 2k + 6k + 5k + 6k + 10k = 1

 30k = 1

⇒ k = 1/30

Therefore the probability mass function is