Chapter: Security in Computing : Designing Trusted Operating Systems
Models of Security
Models of Security
In security and elsewhere,
models are often used to describe, study, or analyze a particular situation or
relationship. McLean [MCL90a] gives a
good overview of models for security. In particular, security models are used
to
·
test a particular policy for completeness and consistency
·
document a policy
·
help conceptualize and design an implementation
·
check whether an implementation meets its requirements
We assume that some access
control policy dictates whether a given user can access a particular object. We
also assume that this policy is established outside any model. That is, a
policy decision determines whether a specific user should have access to a
specific object; the model is only a mechanism that enforces that policy. Thus,
we begin studying models by considering simple ways to control access by one
user.
Multilevel Security
Ideally, we want to build a
model to represent a range of sensitivities and to reflect the need to separate
subjects rigorously from objects to which they should not have access. For
instance, consider an election and the sensitivity of data involved in the
voting process. The names of the candidates are probably not sensitive. If the
results have not yet been released, the name of the winner is somewhat
sensitive. If one candidate received an embarrassingly low number of votes, the
vote count may be more sensitive. Finally, the way a particular individual
voted is extremely sensitive. Users can also be ranked by the degree of
sensitivity of information to which they can have access.
For obvious reasons, the
military has developed extensive procedures for securing information. A
generalization of the military model of information security has also been
adopted as a model of data security within an operating system. Bell and La
Padula [BEL73] were first to describe
the properties of the military model in mathematical notation, and Denning [DEN76a] first formalized the structure of this
model. In 2005, Bell [BEL05] returned to
the original model to highlight its contribution to computer security. He
observed that the model demonstrated the need to understand security requirements
before beginning system design, build security into not onto the system,
develop a security toolbox, and design the system to protect itself. The
generalized model is called the lattice
model of security because its elements form a mathematical structure called
a lattice. (See Sidebar 5-1.) In this
section, we describe the military example and then use it to explain the
lattice model.
Lattice Model of Access Security

Many other structures are
lattices. For example, we noted earlier that a commercial security policy may
contain data sensitivities such as public, proprietary, and internal, with the
natural ordering that public data are less sensitive than proprietary, which
are less sensitive than internal. These three levels also form a lattice.
Security specialists have chosen to base security systems on a
lattice because it naturally represents increasing degrees. A security system
designed to implement lattice models can be used in a military environment.
However, it can also be used in commercial environments with different labels
for the degrees of sensitivity. Thus, lattice representation of sensitivity
levels applies to many computing situations.
BellLa Padula Confidentiality Model
The Bell and La Padula model [BEL73] is a formal description of the allowable
paths of information flow in a secure system. The model's goal is to identify
allowable communication when maintaining secrecy is important. The model has
been used to define security requirements for systems concurrently handling
data at different sensitivity levels. This model is a formalization of the
military security policy and was central to the U.S. Department of Defense's
evaluation criteria, described later in this chapter.
We are interested in secure
information flows because they describe acceptable connections between subjects
and objects of different levels of sensitivity. One purpose for security-level
analysis is to enable us to construct systems that can perform concurrent
computation on data at two different sensitivity levels. For example, we may
want to use one machine for top-secret and confidential data at the same time.
The programs processing top-secret data would be prevented from leaking
top-secret data to the confidential data, and the confidential users would be
prevented from accessing the top-secret data. Thus, the BellLa Padula model is
useful as the basis for the design of systems that handle data of multiple
sensitivities.
In the military model, this property says that
the contents of a sensitive object can be written only to objects at least as
high.
In the military model, one
interpretation of the *-property is that a person obtaining information at one
level may pass that information along only to people at levels no lower than
the level of the information. The *-property prevents write-down, which occurs when a subject with access to high-level
data transfers that data by writing it to a low-level object.
Literally, the *-property
requires that a person receiving information at one level not talk with people
cleared at levels lower than the level of the informationnot even about the
weather! This example points out that this property is stronger than necessary
to ensure security; the same is also true in computing systems. The BellLa
Padula model is extremely conservative: It ensures security even at the expense
of usability or other properties.
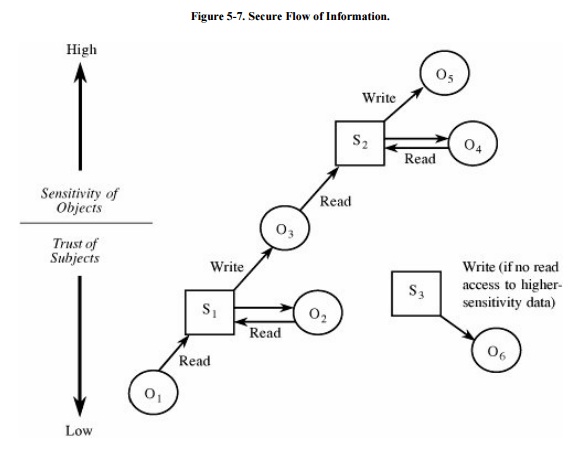
The implications of these two properties are
shown in Figure 5 -7. The
classifications of subjects (represented by squares) and objects (represented
by circles) are indicated by their positions: As the classification of an item
increases, it is shown higher in the figure. The flow of information is
generally horizontal (to and from the same level) and upward (from lower levels
to higher). A downward flow is acceptable only if the highly cleared subject
does not pass any high-sensitivity data to the lower-sensitivity object.
For computing systems,
downward flow of information is difficult because a computer program cannot
readily distinguish between having read a piece of information and having read
a piece of information that influenced what was later written. (McLean [MCL90b], in work related to Goguen and Meseguer [GOG82], presents an interesting counter to the
*-property of Bell and La Padula. He suggests considering noninterference,
which can be loosely described as tracing the effects of inputs on outputs. If
we can trace all output effects, we can determine conclusively whether a
particular low-level output was "contaminated" with high-level
input.)
Biba Integrity Model
The BellLa Padula model
applies only to secrecy of information: The model identifies paths that could
lead to inappropriate disclosure of information. However, the integrity of data
is important, too. Biba [BIB77]
constructed a model for preventing inappropriate modification of data.
The Biba model is the counterpart (sometimes called the dual) of the BellLa Padula model. Biba defines "integrity levels," which are analogous to the sensitivity levels of the BellLa Padula model.
These two rules cover
untrustworthy information in a natural way. Suppose John is known to be
untruthful sometimes. If John can create or modify a document, other people
should distrust the truth of the statements in that document. Thus, an
untrusted subject who has write access to an object reduces the integrity of
that object. Similarly, people are rightly skeptical of a report based on
unsound evidence. The low integrity of a source object implies low integrity
for any object based on the source object.
This model addresses the
integrity issue that the BellLa Padula model ignores. However, in doing so, the
Biba model ignores secrecy. Secrecy-based security systems have been much more
fully studied than have integrity-based systems. The current trend is to join
secrecy and integrity concerns in security systems, although no widely accepted
formal models achieve this compromise.
Models Proving Theoretical Limitations of Security Systems
Models are also useful for
demonstrating the feasibility of an approach. Consider the security properties
that we want a system to have. We want to build a model that tells us (before
we invest in design, code, and testing) whether the properties can actually be
achieved. This new class of models is based on the general theory of
computability, which you may have studied in your computer science classes.
Computability helps us
determine decidability: If we pose a question, we want to know if we will ever
be able to decide what the answer is. The results of these computability-based
models show us the limitations of abstract security systems.
GrahamDenning Model
Lampson [LAM71] and Graham and Denning [GRA72] introduced the concept of a formal system
of protection rules. Graham and Denning constructed a model having generic protection
properties. This model forms the basis for two later models of security
systems.
The GrahamDenning model
operates on a set of subjects S, a set of objects O, a set of rights R, and an
access control matrix A. The matrix has one row for each subject and one column
for each subject and each object. The rights of a subject on another subject or
an object are shown by the contents of an element of the matrix. For each
object, one subject designated the "owner" has special rights; for
each subject, another subject designated the "controller" has special
rights.
The GrahamDenning model has
eight primitive protection rights. These rights are phrased as commands that
can be issued by subjects, with effects on other subjects or objects.
Create object allows the
commanding subject to introduce a new object to the system.
Create subject, delete
object, and delete subject have the similar effect of creating or destroying a
subject or object.
Read access right allows a subject to determine
the current access rights of a subject to an object.
Grant access right allows the
owner of an object to convey any access rights for an object to another
subject.
Delete access right allows a
subject to delete a right of another subject for an object, provided that the deleting
subject either is the owner of the object or controls the subject from which
access should be deleted.
Transfer access right allows
a subject to transfer one of its rights for an object to another subject. Each
right can be transferable or nontransferable. If a subject receives a
transferable right, the subject can then transfer that right (either
transferable or not) to other subjects. If a subject receives a nontransferable
right, it can use the right but cannot transfer that right to other subjects.
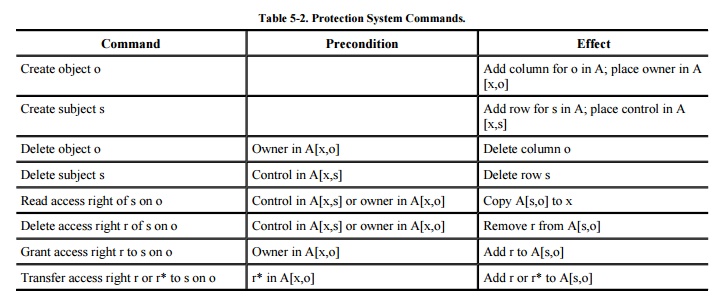
These rules are shown in Table 5-2 (for more details see [GRA72] ), which shows prerequisite conditions
for executing each command and its effect. The access control matrix is A
[s,o], where s is a subject and o is an object. The subject executing each
command is denoted x. A transferable right is denoted r*; a nontransferable
right is written r.
This set of rules provides
the properties necessary to model the access control mechanisms of a protection
system. For example, this mechanism can represent a reference monitor or a
system of sharing between two untrustworthy, mutually suspicious subsystems.
HarrisonRuzzoUllman Results
Harrison, Ruzzo, and Ullman [HAR76] proposed a variation on the GrahamDenning
model. This revised model answered several questions concerning the kinds of
protection a given system can offer. Suppose you are about to use a particular
operating system and you want to know if a given user can ever be granted a
certain kind of access. For example, you may be establishing protection levels
in Windows or MVS. You set up the access controls and then ask whether user X
will ever have access to object Y. The three researchers developed their model
so that we might be able to answer questions like this one.
The HarrisonRuzzoUllman model (called the HRU
model) is based on commands, where
each command involves conditions and
primitive operations. The structure
of a command is as follows.

This command is structured
like a procedure, with parameters o1 through ok. The notation of the HRU model is slightly
different from the
GrahamDenning model; in HRU every subject is an
object, too. Thus, the columns of the access control matrix are all the
subjects and all the objects that are not subjects. For this reason, all the
parameters of a command are labeled o, although they could be either subjects
or nonsubject objects. Each r is a generic right, as in the GrahamDenning
model. Each op is a primitive operation, defined in the following list. The access
matrix is shown in Table 5-3.

The primitive operations op,
similar to those of the GrahamDenning model, are as follows:
·
create subject s
·
create object o
·
destroy subject s
·
destroy object o
·
enter right r into A[s,o]
·
delete right r from A[s,o]
The interpretations of these
operations are what their names imply. A protection
system is a set of subjects, objects, rights, and commands.
Harrison et al. demonstrate
that these operations are adequate to model several examples of protection
systems, including the Unix protection mechanism and an indirect access mode
introduced by Graham and Denning [GRA72].
Thus, like the GrahamDenning model, the HRU model can represent
"reasonable" interpretations of protection.
Two important results derived by Harrison et
al. have major implications for designers of protection systems. We omit the
complete proofs of these results, but we outline them in Sidebar 5-2 to give you an idea of what is
involved.
The first result from HRU
indicates that
In the modeled system, in
which commands are restricted to a single operation each, it is possible to
decide whether a given subject can ever obtain a particular right to an object.
Therefore, we can decide
(that is, we can know in advance) whether a low-level subject can ever obtain
read access to a high-level object, for example.
The second result is less
encouraging. Harrison et al. show that
If
commands are not restricted to one operation each, it is not always decidable
whether a given protection system can confer a given right.
Thus, we cannot determine in
general whether a subject can obtain a particular right to an object.
As an example, consider
protection in the Unix operating system. The Unix protection scheme is
relatively simple; other protection systems are more complex. Because the Unix
protection scheme requires more than one operation per command in the HRU
model, there can be no general procedure to determine whether a certain access
right can be given to a subject.
The HRU result is important but bleak. In fact,
the HRU result can be extended. There may be an algorithm to decide the access
right question for a particular collection of protection systems, but even an
infinite number of algorithms cannot decide the access right question for all
protection systems. However, the negative results do not say that no decision
process exists for any protection system. In fact, for certain specific
protection systems, it is decidable whether a given access right can be
conferred.
Sidebar
5-2: Proving the HRU Results
The first HRU result applies when
commands are restricted to containing just one operation each. In this case, it
is possible to decide whether a given protection system, started with a given
initial configuration of the access control matrix, can allow a given user a
given access right to a given object. In other words, suppose you want to know whether a
particular protection system can allow a subject s to obtain access right r to
object o. (Harrison et al. say that such a system leaks the access right.)
As long as
each command consists of only a single operation, there is an algorithm that
can answer this question. The proof involves analyzing the minimum number of
commands by which a right can be conferred. Certain operations, such as delete
and destroy, have no effect on expanding access rights; they can be ignored.
The shortest sequence of commands by which such a right can be conferred
contains at most m = | r | * ( |s|+1) *( |o|+1) + 1 commands, where | r | is
the number of rights, |s| is the number of subjects, and |o| is the number of
objects in the protection system. The algorithm
calls for
testing all sequences of commands of length up to m. (There are 2km
such sequences, for some constant k.) If the right is conferred, it will be in
one of the sequences.
The proof of the second HRU result uses commands of an HRU protection
system to represent operations of a formal system called a Turing machine.
Turing machines are general models of computing devices, expressed as a machine
reading a tape that has a string of zeros and ones. The decidability problems
we want to solve are often framed so that the result we seek is true if we can
decide whether the Turing machine will ever halt when reading commands from the
tape. Any conventional computing system and program can be modeled with a
Turing machine. Several decidable results about Turing machines are well known,
including one that shows it is impossible to develop a general procedure to
determine whether a given Turing machine will halt when performing a given
computation. The proof of the second HRU result follows by the demonstration
that a decision procedure for protection systems would also solve the halting
problem for Turing machines, which is known to be unsolvable.
Therefore, the HRU results
are negative for general procedures but do not rule out the possibility of
making decisions about particular protection systems.
TakeGrant Systems
One final model of a
protection system is the takegrant
system, introduced by Jones [JON78a] and
expanded by Lipton and Snyder [LIP77, SNY81].
This model has only four
primitive operations: create, revoke, take, and grant. Create and revoke are
similar to operations from the GrahamDenning and HRU models; take and grant are
new types of operations. These operations are presented most naturally through
the use of graphs.
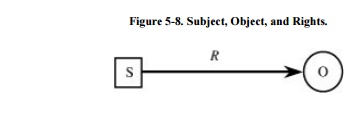
As in other systems, let S be a set of subjects
and O be a set of objects; objects can be either active (subjects) or passive
(nonsubject objects). Let R be a set of rights. Each subject or object is
denoted by a node of a graph; the rights of a particular subject to a
particular object are denoted by a labeled, directed edge from the subject to
the object. Figure 5-8 shows an example
of subject, object, and rights.
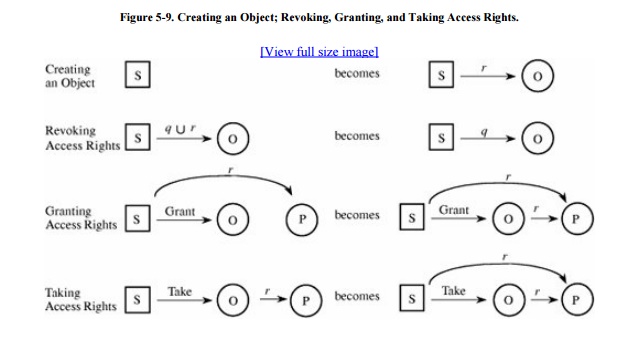
Let s be the subject performing each of the
operations. The four operations are defined as follows. The effects of these
operations are shown in Figure 5-9.
Snyder shows that in this system certain protection questions are decidable; furthermore, they are decidable in reasonable (less than exponential) time. In [SNY81], Snyder considers two questions:
1. Can we decide whether a given subject can share an object with another subject?
Clearly, these are important
questions to answer about a protection system, for they show whether the access
control mechanisms are secure against unauthorized disclosure.
The answer to Snyder's first
question is yes. Sharing can occur only if several other subjects together have
the desired access to the object and the first subject is connected to each of
the group of other subjects by a path of edges having a particular form. An
algorithm that detects sharability runs in time proportional to the size of the
graph of the particular case.
Snyder also answers the
second question affirmatively, in a situation heavily dependent on the ability
to share. Thus, an algorithm can decide whether access can be stolen by direct
appeal to the algorithm to decide sharability.
Landwehr [LAN81] points out that the takegrant model
assumes the worst about users: If a user can grant access rights, the model
assumes that the user will. Suppose a user can create a file and grant access
to it to everyone. In that situation, every user could allow access to every
object by every other user. This worst-case assumption limits the applicability
of the model to situations of controlled sharing of information. In general,
however, the takegrant model is useful because it identifies conditions under
which a user can obtain access to an object.
Summary of Models of Protection Systems
We study models of computer
security for two reasons. First, models are important in determining the
policies a secure system should enforce. For example, the BellLa Padula and
Biba models identify specific conditions we must enforce so that we can ensure
secrecy or integrity. Second, the study of abstract models can lead to an
understanding of the properties of protection systems. For example, the HRU
model states certain characteristics that can or cannot be decided by an
arbitrary protection system. These characteristics are important for designers
of protection systems to know.
Building and analyzing models are essential to
designing a trusted operating system. We use models of protection systems to
establish our security policies, determining what is feasible and desirable
from what is not. From the policies we move to the operating system design
itself. In the next section, we look closely at trusted operating system
design.
Related Topics