Assurance Methods

Assurance Methods

Once we understand the potential vulnerabilities in a system, we can apply assurance techniques to seek out the vulnerabilities and mitigate or eliminate their effects. In this section, we consider three such techniques, showing how they give us confidence in a system's correctness: testing, verification, and validation. None of these is complete or foolproof, and each has advantages and disadvantages. However, used with understanding, each can play an important role in deriving overall assurance of the systems' security.

Testing

Testing, first presented in Chapter 3, is the most widely accepted assurance technique. As Boebert [BOE92] observes, conclusions from testing are based on the actual product being evaluated, not on some abstraction or precursor of the product. This realism is a security advantage. However, conclusions based on testing are necessarily limited, for the following reasons:

  Testing can demonstrate the existence of a problem, but passing tests does not demonstrate the absence of problems.

  Testing adequately within reasonable time or effort is difficult because the combinatorial explosion of inputs and internal states makes testing very complex.

  Testing based only on observable effects, not on the internal structure of a product, does not ensure any degree of completeness.

  Testing based on the internal structure of a product involves modifying the product by adding code to extract and display internal states. That extra functionality affects the product's behavior and can itself be a source of vulnerabilities or mask other vulnerabilities.

Testing real-time or complex systems presents the problem of keeping track of all states and triggers. This problem makes it hard to reproduce and analyze problems reported as testers proceed.

Ordinarily, we think of testing in terms of the developer: unit testing a module, integration testing to ensure that modules function properly together, function testing to trace correctness across all aspects of a given function, and system testing to combine hardware with software. Likewise, regression testing is performed to make sure a change to one part of a system does not degrade any other functionality. But for other tests, including acceptance tests, the user or customer administers tests to determine if what was ordered is what is delivered. Thus, an important aspect of assurance is considering whether the tests run are appropriate for the application and level of security. The nature and kinds of testing reflect the developer's testing strategy: which tests address what issues.

Similarly, it is important to recognize that testing is almost always constrained by a project's budget and schedule. The constraints usually mean that testing is incomplete in some way. For this reason, we consider notions of test coverage, test completeness, and testing effectiveness in a testing strategy. The more complete and effective our testing, the more confidence we have in the software. More information on testing can be found in Pfleeger and Atlee [PFL06a].

Penetration Testing

A testing strategy often used in computer security is called penetration testing, tiger team analysis, or ethical hacking. In this approach, a team of experts in the use and design of operating systems tries to crack the system being tested. (See, for example, [RUB01, TIL03, PAL01].) The tiger team knows well the typical vulnerabilities in operating systems and computing systems, as described in previous sections and chapters. With this knowledge, the team attempts to identify and exploit the system's particular vulnerabilities. The work of penetration testers closely resembles what an actual attacker might do [AND04, SCH00b].

Penetration testing is both an art and a science. The artistic side requires careful analysis and creativity in choosing the test cases. But the scientific side requires rigor, order, precision, and organization. As Weissman observes [WEI95], there is an organized methodology for hypothesizing and verifying flaws. It is not, as some might assume, a random punching contest.

Using penetration testing is much like asking a mechanic to look over a used car on a sales lot. The mechanic knows potential weak spots and checks as many of them as possible. It is likely that a good mechanic will find significant problems, but finding a problem (and fixing it) is no guarantee that no other problems are lurking in other parts of the system. For instance, if the mechanic checks the fuel system, the cooling system, and the brakes, there is no guarantee that the muffler is good. In the same way, an operating system that fails a penetration test is known to have faults, but a system that does not fail is not guaranteed to be fault-free. Nevertheless, penetration testing is useful and often finds faults that might have been overlooked by other forms of testing. One possible reason for the success of penetration testing is its use under real-life conditions. Users often exercise a system in ways that its designers never anticipated or intended. So penetration testers can exploit this real-life environment and knowledge to make certain kinds of problems visible.

Penetration testing is popular with the commercial community who think skilled hackers will test (attack) a site and find problems in hours if not days. These people do not realize that finding flaws in complex code can take weeks if not months. Indeed, the original military red teams to test security in software systems were convened for 4- to 6-month exercises. Anderson et al. [AND04] point out the limitation of penetration testing. To find one flaw in a space of 1 million inputs may require testing all 1 million possibilities; unless the space is reasonably limited, this search is prohibitive. Karger and Schell [KAR02] point out that even after they informed testers of a piece of malicious code they inserted in a system, the testers were unable to find it. Penetration testing is not a magic technique for finding needles in haystacks.

Formal Verification

The most rigorous method of analyzing security is through formal verification, which was introduced in Chapter 3 . Formal verification uses rules of mathematical logic to demonstrate that a system has certain security properties. In formal verification, the operating system is modeled and the operating system principles are described as assertions. The collection of models and assertions is viewed as a theorem, which is then proven. The theorem asserts that the operating system is correct. That is, formal verification confirms that the operating system provides the security features it should and nothing else.

Proving correctness of an entire operating system is a formidable task, often requiring months or even years of effort by several people. Computer programs called theorem provers can assist in this effort, although much human activity is still needed. The amount of work required and the methods used are well beyond the scope of this book. However, we illustrate the general principle of verification by presenting a simple example that uses proofs of correctness. You can find more extensive coverage of this topic in [BOW95], [CHE81], [GRI81], [HAN76], [PFL06a], and [SAI96].

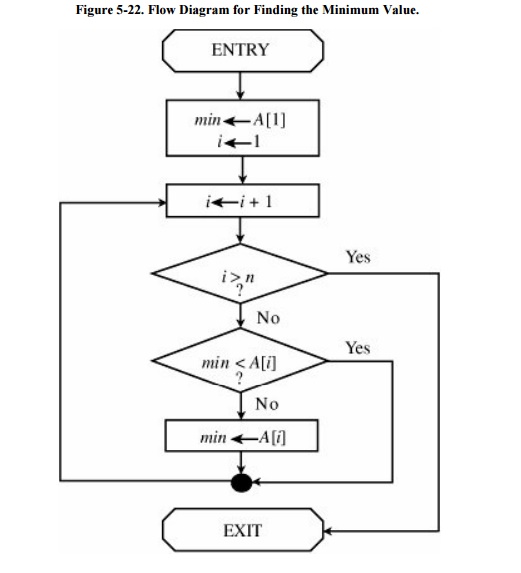
Consider the flow diagram of Figure 5-22, illustrating the logic in a program to determine the smallest of a set of n values, A[1] through A [n]. The flow chart has a single identified beginning point, a single identified ending point, and five internal blocks, including an if-then structure and a loop.

In program verification, we rewrite the program as a series of assertions about the program's variables and values. The initial assertion is a statement of conditions on entry to the module. Next, we identify a series of intermediate assertions associated with the work of the module. We also determine an ending assertion, a statement of the expected result. Finally, we show that the initial assertion leads logically to the intermediate assertions that in turn lead logically to the ending assertion.

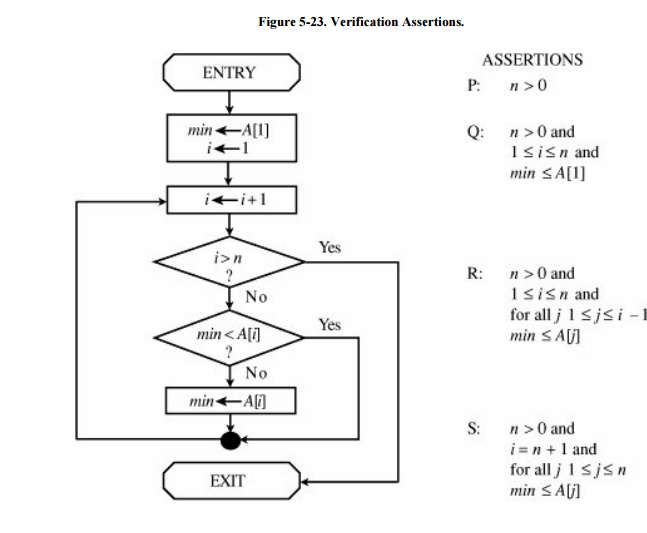
We can formally verify the example in Figure 5-22 by using four assertions. The first assertion, P, is a statement of initial conditions, assumed to be true on entry to the procedure.

These four assertions, shown in Figure 5 -23, capture the essence of the flow chart. The next step in the verification process involves showing the logical progression of these four assertions. That is, we must show that, assuming P is true on entry to this procedure, Q is true after completion of the initialization section, R is true the first time the loop is entered, R is true each time through the loop, and the truth of R implies that S is true at the termination of the loop.

Clearly, Q follows from P and the semantics of the two statements in the second box. When we enter the loop for the first time, i = 2, so i - 1 = 1. Thus, the assertion about min applies only for j = 1, which follows from Q. To prove that R remains true with each execution of the loop, we can use the principle of mathematical induction. The basis of the induction is that R was true the first time through the loop. With each

The algorithm (not the verification) shown here is frequently used as an example in the first few weeks of introductory programming classes. It is quite simple; in fact, after studying the algorithm for a short time, most students convince themselves that the algorithm is correct. The verification itself takes much longer to explain; it also takes far longer to write than the algorithm itself. Thus, this proof-of-correctness example highlights two principal difficulties with formal verification methods:

z        Time. The methods of formal verification are time consuming to perform. Stating the assertions at each step and verifying the logical flow of the assertions are both slow processes.

  Complexity. Formal verification is a complex process. For some systems with large numbers of states and transitions, it is hopeless to try to state and verify the assertions. This situation is especially true for systems that have not been designed with formal verification in mind.

These two difficulties constrain the situations in which formal verification can be used successfully. Gerhart [GER89] succinctly describes the advantages and disadvantages of using formal methods, including proof of correctness. As Schaefer [SCH89a] points out, too often people focus so much on the formalism and on deriving a formal proof that they ignore the underlying security properties to be ensured.

Validation

Formal verification is a particular instance of the more general approach to assuring correctness: verification. As we have seen in Chapter 3, there are many ways to show that each of a system's functions works correctly. Validation is the counterpart to verification, assuring that the system developers have implemented all requirements. Thus, validation makes sure that the developer is building the right product (according to the specification), and verification checks the quality of the implementation [PFL06a]. There are several different ways to validate an operating system.

  Requirements checking. One technique is to cross-check each operating system requirement with the system's source code or execution-time behavior. The goal is to demonstrate that the system does each thing listed in the functional requirements. This process is a narrow one, in the sense that it demonstrates only that the system does everything it should do. In security, we are equally concerned about prevention: making sure the system does not do the things it is not supposed to do. Requirements checking seldom addresses this aspect of requirements compliance.

  Design and code reviews. As described in Chapter 3, design and code reviews usually address system correctness (that is, verification). But a review can also address requirements implementation. To support validation, the reviewers scrutinize the design or the code to ensure traceability from each requirement to design and code components, noting problems along the way (including faults, incorrect assumptions, incomplete or inconsistent behavior, or faulty logic). The success of this process depends on the rigor of the review.

  System testing. The programmers or an independent test team select data to check the system. These test data can be organized much like acceptance testing, so behaviors and data expected from reading the requirements document can be confirmed in the actual running of the system. The checking is done in a methodical manner to ensure completeness.