Minimizing the Overall Variance

Minimizing the Overall Variance

A final consideration in developing a sampling plan is to minimize the overall vari- ance for the analysis. Equation 7.2 shows that the overall variance is a function of the variance due to the method and the variance due to sampling. As we have seen, we can improve the variance due to sampling by collecting more samples of proper size. Increasing the number of times we analyze each sample improves the variance due to the method. If s_s2 is significantly greater than s_m2 , then the method’s variance can be ignored and equation 7.7 used to estimate the number of samples to analyze. Analyzing any sample more than once will not improve the overall variance, since the variance due to the method is insignificant.

If s_m2 is significantly greater than s_s2, then we only need to collect and analyze a single sample. The number of replicate analyses, n_r, needed to minimize the error due to the method is given by an equation similar to equation 7.7

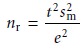
Unfortunately, the simple situations just described are often the exception. In many cases, both the sampling variance and method variance are significant, and both multiple samples and replicate analyses of each sample are required. The over- all error in this circumstance is given by

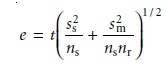                    7.8

Equation 7.8 does not have a unique solution because different combinations of n_s and n_r give the same overall error. The choice of how many samples to collect and how many times each sample should be analyzed is determined by other concerns, such as the cost of collecting and analyzing samples, and the amount of available sample.