Chapter: Modern Analytical Chemistry: Obtaining and Preparing Samples for Analysis
How Many Samples to Collect
How Many Samples to Collect
In the previous
section we considered the amount of sample needed
to minimize the sampling
variance. Another important
consideration is the number of samples
required to achieve a desired
maximum sampling error. If samples
drawn from the target population are normally
distributed, then the following equation describes the confidence interval for the sampling
error
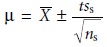
where ns is
the number of samples and ss
is the sampling standard deviation. Rear- ranging and substituting e for
the quantity (μ– X–), gives the
number of samples as
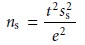 7.7
7.7
where ss2 and e2 are both expressed as absolute uncertainties or as relative uncertain- ties. Finding a solution to equation 7.7
is complicated by the fact
that the value
of t depends on ns. As shown in Example 7.8, equation 7.7 is solved
iteratively.

This is not an uncommon
problem. For a target population with a relative
sampling variance of 50 and a desired relative
sampling error of ±5%, equation
7.7 predicts that ten
samples are sufficient. In a simulation in which 1000
samples of size
10 were collected, however,
only 57% of the samples
resulted in sampling
errors of less than ±5%. By increasing the
number of samples
to 17 it was possible to ensure that the desired sampling error
was achieved 95% of the time.
Related Topics