How Much Sample to Collect

How Much Sample to Collect

To minimize sampling errors, a randomly collected grab sample must be of an ap- propriate size. If the sample is too small its composition may differ substantially from that of the target population, resulting in a significant sampling error. Samples that are too large, however, may require more time and money to collect and ana- lyze, without providing a significant improvement in sampling error.

As a starting point, let’s assume that our target population consists of two types of particles. Particles of type A contain analyte at a fixed concentration, and type B particles contain no analyte. If the two types of particles are randomly distributed, then a sample drawn from the population will follow the binomial distribution.* If we collect a sample containing n particles, the expected number of particles con- taining analyte, n_A, is

n_A = np

where p is the probability of selecting a particle of type A. The sampling standard deviation is

Note that the relative sampling variance is inversely proportional to the number of particles sampled. Increasing the number of particles in a sample, therefore, im- proves the sampling variance.

A sample containing 1013 particles can be fairly large. Suppose this is equivalent to a mass of 80 g. Working with a sample this large is not practical; but does this mean we must work with a smaller sample and accept a larger relative sampling variance? Fortunately the answer is no. An important feature of equation 7.4 is that the relative sampling variance is a function of the number of particles but not their combined mass. We can reduce the needed mass by crushing and grinding the par- ticles to make them smaller. Our sample must still contain 1013 particles, but since each particle is smaller their combined mass also is smaller. If we assume that a par- ticle is spherical, then its mass is proportional to the cube of its radius.

Mass ∝ r3

Decreasing a particle’s radius by a factor of 2, for example, decreases its mass by a fac- tor of 23, or 8. Instead of an 80-g sample, a 10-g sample will now contain 1013 particles.

Treating a population as though it contains only two types of particles is a use- ful exercise because it shows us that the relative sampling variance can be improved by collecting more particles of sample. Furthermore, we learned that the mass of sample needed can be reduced by decreasing particle size without affecting the rela- tive sampling variance. Both are important conclusions.

Few populations, however, meet the conditions for a true binomial distribu- tion. Real populations normally contain more than two types of particles, with the analyte present at several levels of concentration. Nevertheless, many well-mixed populations, in which the population’s composition is homogeneous on the scale at which we sample, approximate binomial sampling statistics. Under these conditions the following relationship between the mass of a randomly collected grab sample, m, and the percent relative standard deviation for sampling, R, is often valid.

mR2 = K_s

where K_s is a sampling constant equal to the mass of sample producing a percent relative standard deviation for sampling of ±1%.* The sampling constant is evalu- ated by determining R using several samples of similar mass. Once K_s is known, the mass of sample needed to achieve a desired relative standard deviation for sampling can be calculated.

When the target population is segregated, or stratified, equation 7.5 provides a poor estimate of the amount of sample needed to achieve a desired relative standard de- viation for sampling. A more appropriate relationship, which can be applied to both segregated and nonsegregated samples, has been proposed.

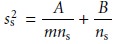                     7.6

where n_s is the number of samples to be analyzed, m is the mass of each sample, A is a homogeneity constant accounting for the random distribution of analyte in the target population, and B is a segregation constant accounting for the nonrandom distribution of analyte in the target population. Equation 7.6 shows that sampling variance due to the random distribution of analyte can be minimized by increasing either the mass of each sample or the total number of samples. Sampling errors due to the nonrandom distribution of the analyte, however, can only be minimized by increasing the total number of samples. Values for the homogeneity constant and heterogeneity constant are determined using two sets of samples that differ signifi- cantly in mass.