General Theory of Separation Efficiency

General Theory of Separation Efficiency

The goal of an analytical separation is to remove either the analyte or the interferent from the sample matrix. To achieve a separation there must be at least one signifi- cant difference between the chemical or physical properties of the analyte and inter- ferent. Relying on chemical or physical properties, however, presents a fundamental problem—a separation also requires selectivity. A separation that completely re- moves an interferent may result in the partial loss of analyte. Altering the separation to minimize the loss of analyte, however, may leave behind some of the interferent.

A separation’s efficiency is influenced both by the failure to recover all the ana- lyte and the failure to remove all the interferent. We define the analyte’s recovery, R_A, as

where C_A is the concentration of analyte remaining after the separation, and (C_A)_o is the analyte’s initial concentration. A recovery of 1.00 means that none of the ana- lyte is lost during the separation. The recovery of the interferent, R_I, is defined in the same manner

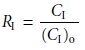           7.13

where C_I is the concentration of interferent remaining after the separation, and (C_I)_o is the interferent’s initial concentration. The degree of separation is given by a separation factor, S_I,A, which is the change in the ratio of interferent to analyte caused by the separation.

In an ideal separation R_A = 1, R_I = 0, and S_I,A = 0. In general, the separation factor should be approximately 10–7 for the quantitative analysis of a trace analyte in the presence of a macro interferent, and 10–3 when the analyte and interferent are pres- ent in approximately equal amounts.

Recoveries and separation factors are useful ways to evaluate the effectiveness of a separation. They do not, however, give a direct indication of the relative error introduced by failing to remove all interferents or failing to recover all the analyte. The relative error introduced by the separation, E, is defined as

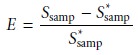            7.14

A more useful equation for the relative error is obtained by solving equation 7.13 for C_I and substituting back into equation 7.16

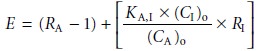                                   7.17

The first term of equation 7.17 accounts for the incomplete recovery of analyte, and the second term accounts for the failure to remove all the interferent.