Feed formulation and feed formulae - Artificial feeds

Feed formulation and feed formulae

The primary objective of feed formulation is to provide the species under culture with an acceptable diet that meets its nutritional requirements at different stages of its life, so as to yield optimum production at minimum cost. As has already been pointed out, our present knowledge of the nutritional needs of aquatic animals is restricted to only a few species, and feed formulation for other species has to be approximated on this basis. Although it is most likely that all aquaculture species can be weaned to consume processed compound feeds, there is still a lot to be learnt about the physical and chemical properties of diets preferred by several species. Flavour, colour,

odour, texture and water stability are important characteristics related to acceptance and consumption. Better knowledge of preferences and feeding behaviour would greatly improve the choice of appropriate ingredients and feed preparation processes, as well as the methods of feed dispensing.

For formulating the basic composition of a feed, the main information needed are the levels of crude protein, energy, specific amino acids, crude fibre and ash required. The energy level may be in terms of metabolizable energy

(ME) or digestible energy (DE). Most complete practical diets have to be supplemented with a vitamin premix, at levels in excess of the dietary requirement. All levels, with the exception of energy, are determined on the basis of chemical tests on samples of a feedstuff. Even though they correlate well with biological methods of feed evaluation, such as growth studies, tissue levels, etc., they are subject to errors due to variability in composition. For example, the proximate composition of fish meal made from spawning fish is different from that made from immature fish. Usually, the lipid levels increase before spawning and decrease afterwards, changing the percentage compositions of protein, ash and carbohydrates. Many plant feedstuffs also show compositional variations according to season, locality and environment. However, formulations have often to be based on average values.

Another problem to be considered is seasonality in the availability of ingredients. It may not always be possible to store large quantities of ingredients, and so it becomes necessary to vary ingredient composition according to availability. In many developing countries where feedstuffs are scarce, one cannot expect sufficient priority to be given to their use in aquaculture. Even when a particular feedstuff is available for purchase, increased prices may make it necessary to use substitutes in order to obtain a least-cost ration. It therefore follows that there are no fixed formulae for feeds and that they have to vary according to availability of ingredients, composition and costs. Least-cost feeds have to be formulated, but in doing so careful consideration has to be given to the quality of the nutrient content in substitute ingredients. Changes of ingredients or their proportions may also affect the physical characteristics and palatability of the diets. So feed costs should be estimated not on the basis of the price of ingredients alone, but also on the proportion of feed costs in the overall production cost per unit weight of fish.

The type of feed required and the methods of processing will influence formulation. Extruded or floating-type feeds must contain an appreciable quantity of starch for satisfactory gelatinization and expansion. Most such feeds contain 20–25 per cent cereal grain such as corn, wheat or sorghum. Again, depending on the storage conditions and duration of storage, a certain amount of loss of vitamins has to be expected. In order to cover such loss, it will be necessary to add higher levels of vitamins than are nutritionally required.

The type of culture system also has a determining role in feed formulation. For example, if the feed is for use in semi-intensive pond culture, certain vitamin and mineral supplements can be omitted from the formula, as these nutrients are likely to be available to the animal from the natural food organisms growing in the ponds. On the other hand, in intensive culture in cages, raceways and tanks, where natural foods are limited, the diet should contain all the required nutrients in adequate quantities and proportions. Similarly, when the feed is meant to be used as supplementary feed, to augment the major nutritional elements provided by natural food, the formulations will have to be based on the quantitative assessment of additional requirements of these elements. The problems of formulating supplementary feeds were mentioned.

Since protein is the most expensive portion of an animal diet, it is usually computed first in diet formulation. The first step consists of balancing the crude protein and energy levels. Then the levels of indispensable amino acids should be assessed to ensure that the animal’s dietary levels in this respect are met. Except in the case of unconventional protein supplements, if the feedstuff has the required dietary levels of arginine, lysine, methionine and tryptophan it is most likely that the other six indispensable amino acids are above required levels (Hardy, 1980). In cases where the formulation is low in amino acids, necessary alterations have to be made by the addition of ingredients with

high levels of the required amino acids. After this is done, a final check will be necessary to ensure that the balance of protein and energy levels is not altered.

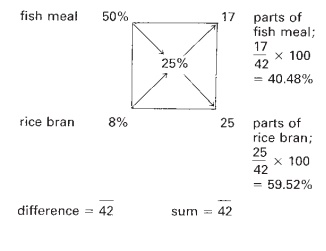
The most commonly used methods for balancing crude protein levels are the square method and algebraic equations. For example, to balance a supplementary feed to contain 25 per cent protein, using only two ingredients – fish meal (50 per cent protein) and rice bran (8 per cent protein) – a square is constructed as shown above. The desired protein level of the feed (25 per cent) is inserted in its centre. The two feedstuffs, along with their protein content, are placed on each corner at the left-hand side of the square and the levels of protein of each feedstuff are subtracted from the desired protein level of the feed. The differences are placed on the corners of the square diagonally opposite the feedstuff, ignoring plus or minus signs (see diagram). The difference between the percentages of protein in the rice bran and the protein required in the feed under formulation show the proportion of fish meal needed. The difference between the protein percentage of fish meal and of the feed being formulated show the proportion of rice bran required. These proportions can be expressed on a percentage basis, as 40.48 per cent fish meal and 59.52 per cent rice bran, or as a ratio of 17 parts: 25 parts.

Algebraic equations can be used to arrive at the same percentages as follows:

assume

x =fish meal in kg per 100 kg feed

 y =rice bran in kg per 100 kg feed

In actual practice, more than two ingredients are generally used in feed formulations. The use of both the square method and algebraic equations is illustrated in the following example to balance a diet containing 30 per cent protein using fish meal (60 per cent protein), soybean mean (51 per cent protein), rice bran (8 per cent protein) and corn meal (10 per cent protein) in the proportions 2 parts soybean meal: 1 part fish meal and 1 part rice bran to 1 part corn meal.

Using the square method as in the above example, the desired protein level (30 per cent) is placed in the middle of the square. The ingre-dients are separated into two groups and the protein level of each group calculated according to the proportion specified:

protein source: fish meal = 1 x 60 = 60%

soybean meal = 2 x 51 = 102%

average = 162/3 = 54%

energy source: rice bran = 1 x 8 = 8% corn meal = 1 x 10 = 10%

average = 18/2 = 9%

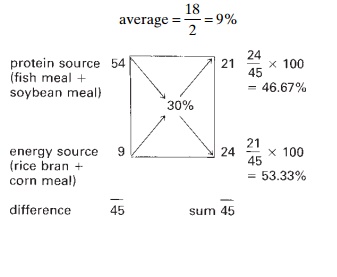
The protein and energy sources, along with their calculated protein contents are placed on each corner at the left-hand side of the square. After diagonal subtraction, the calculation proceeds as shown below. The final figure for the protein source is divided into 2/3 soybean meal and 1/3 fish meal:

protein source = 46.67 per cent

If the algebraic equation method is used, the ingredients are separated into two groups and the protein level of each group calculated according to the proportion required:

Very often, more complicated formulations than the ones described above will become necessary. For example, the diet may have to be for-mulated to contain specified amounts of certain feedstuffs and concentrations of various nutrients, as in the following example (Lim, 1982).

An allplant diet has to be made using soybean meal and peanut meal in the ratio 1 : 1 as protein source, with the following nutrient specifications:

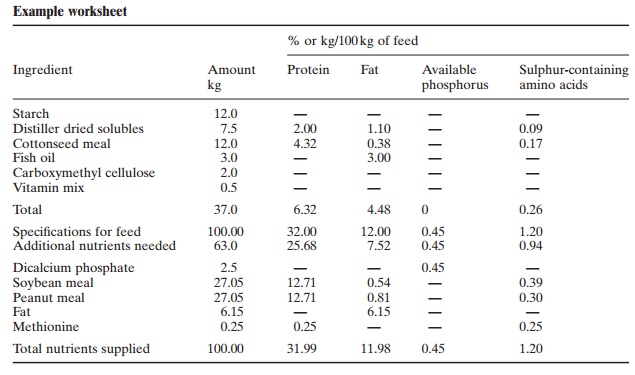
The composition of the available ingredients is listed in Table 7.24. The formulation proceeds as follows. A work sheet (as shown in the example) is made up and the required feed ingredients and amounts filled in first.The nutrients that will be furnished by these ingredients are calculated as a percentage (or kg per 100kg feed) according to available data on their nutrient composition. By adding up the items, the total amounts of each nutrient supplied by the feedstuffs are obtained. By subtracting these amounts from the level of nutrients required in the formulated feed, the additional amounts of nutrients needed and the quantities of other ingredients to provide those nutrients are deter-mined.As soybean meal and peanut meal do not contain any available phosphorus, dicalcium phosphate should be added. As dicalcium

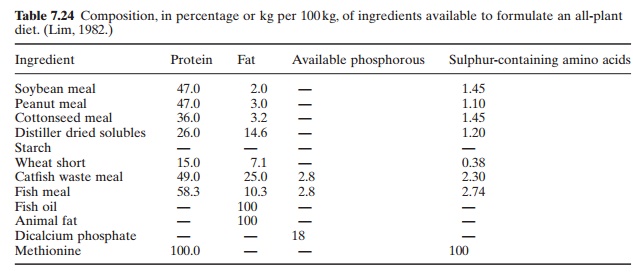
phosphate contains 18 per cent available phosphorus, the required quantity per 100 kg is 0.45/ 0.18 = 2.5 kg. This leaves 100 - 39.5 = 60.5 kg per 100 kg (or per cent) of other ingredients. If this is to be supplied by soybean meal and peanut meal in equal proportions, the nutrients will be provided by 2.44 kg protein, 1.51 kg fat and 0.77 kg sulphur-containing amino acids per 100 kg.Since these do not meet the full requirements for fat and sulphur-containing amino acids, animal fat and methionine have to be added. The same results can be obtained by using algebraic equations.

Linear programming in feed formulation is a mathematical procedure to obtain the optimum solution to specified objectives. It is of special importance in least-cost ration formulation, as there are many ingredients that can provide the necessary protein levels in a ration and there may be a need to change ingredients according to availability, price and quality. While there may be several possible solutions to achieving a given set of specifications, there will be one formulation that costs the least. This elaborate calculation involes the simultaneous solution of a number of linear equations and can best be

done with a computer. It is widely practised in livestock and poultry feed manufacture and has been used in the manufacture of fish feeds.

For formulation of least-cost rations, the computer should have the ration specifications together with the nutrient requirements of the animal. The critical nutrients such as methion-ine and lysine are specified as minimum, range, ration or exact amounts. Nutrients, such as trace elements and vitamins, which are supplied at constant levels need not be indicated. Relevant specifications of the feedstuffs to be used should be put in, along with the composition and price of various available feedstuffs to be included in the formula. Since the accuracy of the formula will depend on the exact nutrient composition of the feedstuffs to be used, the values should be as accurate as possible. Prices used should be those at the time and point where the feed is made, in order to obtain a realistic and effective least-cost ration. By expressing these various data inputs as constraints or restrictions, a series of linear equations are formed. Successful solution of the various simultaneous linear equations leads to an optimal solution. When erroneous ingredient data are used or when unreasonable restrictions are placed on nutrient requirements or ingredient usage, the computer may report that a solution is not feasible. This normally happens only when there are errors in data input. It is therefore essential to check the information thoroughly and input only precise data.