Determination and Calculation of lattice enthalpy of NaCl

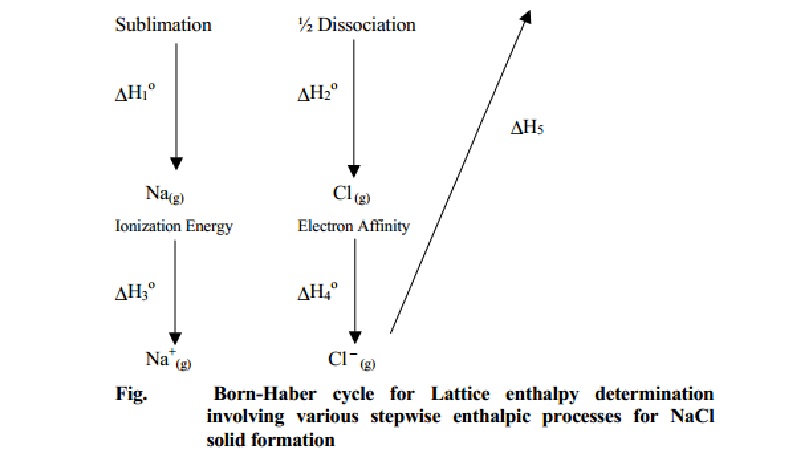
Born Haber's Cycle

Determination of Lattice enthalpy

It is not possible to calculate the lattice enthalpy directly from the forces of attraction and repulsion between ions but factors associated with crystal geometry must also be included. The solid crystal is a three-dimensional entity. The lattice enthalpy is indirectly determined by the use of Born - Haber Cycle. The procedure is based on Hess's law, which states that the enthalpy change of a reaction is the same at constant volume and pressure whether it takes place in a single or multiple steps long as the initial reactants and the final products remain the same. Also it is assumed that the formation of an ionic compound may occur either by direct combination of elements (or) by a step wise process involving vaporisation of elements, conversion of gaseous atoms into ions and the combination of the gaseous ions to form the ionic solid.

For example consider the formation of a simple ionic solid such as an alkali metal halide MX, the following steps are considered.

M_(s)--- (∆ H⁰₍₁₎ )--- > M_(g) --- (∆ H⁰₍₃₎ )--- > M⁺_(g) + e

M_(s) + ½ X_2(g) --- (∆ H⁰₍₂₎ )- > X_(g) -- (∆ H⁰₍₄₎ , +e ) -- > X^-_(g)+ M⁺_(g) ---- > MX_(s) --- (∆ H⁰_(f) ) -- >  ½ X_2(g)

∆ H⁰₍₁₎ =      enthalpy change for sublimation of M(s) to M(g)

∆ H⁰₍₂₎ =      enthalpy change for dissociation of 1/2 X_2(g) to X_(g)

∆ H⁰₍₃₎ =      ionization energy of M_(g) to M⁺_(g)

∆ H⁰₍₄₎ =      electronic affinity or electron gain energy for conversion of X_(g) to X^-_(g)

∆ H⁰₍₅₎ =      the lattice enthalpy for formation of solid MX (1 mole).

∆ H⁰_(f) =       enthalpy change for formation of MX solid directly from the respective elements such as 1 mole of solid M and 0.5 moles of X2(g).

∆ H⁰_(f) =  ∆ H⁰₍₁₎    + ∆ H⁰₍₂₎   + ∆ H⁰₍₃₎   + ∆ H⁰₍₄₎   + ∆ H⁰₍₅₎  

Some important features of lattice enthalpy are:

 The greater the lattice enthalpy the more stabler the ionic bond formed.

 The lattice enthalpy is greater for ions of higher charge and smaller radii.

 The lattice enthalpies affect the solubilities of ionic compounds.

Calculation of lattice enthalpy of NaCl

Let us use the Born - Haber cycle for determining the lattice enthalpy of NaCl as follows :

_{The standard enthalpy change,} ∆ H⁰_(f) overall for the reaction,

Na(s) + 1/2 Cl2(g) → NaCl(s) is - 411.3 kJmol-1

Na(s) + ½ Cl 2(g) --- (∆f Ho ) -- > NaCl(s)

Since the reaction is carried out with reactants in elemental forms and products in their standard states, at 1 bar, the overall enthalpy change of the reaction is also the enthalpy of formation for NaCl. Also, the formation of NaCl can be considered in 5 steps.The sum of the enthalpy changes of these steps is considered equal to the enthalpy change for the overall reaction from which the lattice enthalpy of NaCl is calculated.

Atomisation         :

  ∆ H⁰₍₁₎ for Na(s) → Na(g) is + 108.70 (kJ mol¹)

Dissociation:

∆ H⁰₍₂₎  for ½ Cl₂(g) -- -- > Cl(g) is + 122.0

Ionisation :

∆ H⁰₍₃₎  for Na(g)  -- -- >  Na⁺(g) + e is + 495.0

Electron affinity :

∆ H⁰₍₄₎  for e + Cl(g) -- -- >  Cl^- (g) is - 349.0

Lattice enthalpy :

∆ H⁰₍₁₎  for Na⁺(g) + Cl^-(g)       -- -- > NaCl(g) is ?

∆ H⁰_(f) =  ∆ H⁰₍₁₎    + ∆ H⁰₍₂₎   + ∆ H⁰₍₃₎   + ∆ H⁰₍₄₎   + ∆ H⁰₍₅₎  

∆ H⁰₍₅₎ = -788.0 kj mol^-1

But the lattice enthalpy of NaCl is defined by the reaction

NaCl(g) → Na+ (g) + Cl- (g) only.

Lattice enthalpy value from ∆ H⁰₍₅₎ is written with a reversed sign.

∴ Lattice enthalpy of NaCl = +788.0 kJ mol-1.