Chapter: 11th Chemistry : UNIT 3 : Periodic Classification of Elements
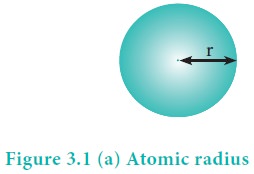
Atomic radius
Atomic radius
Atomic radius of an atom is defined as the distance between the centre of its nucleus and the outermost shell containing the valence electron.
It is not possible to measure the radius of an isolated atom directly. Except for noble gases, usually atomic radius is referred to as covalent radius or metallic radius depending upon the nature of bonding between the concerned atoms.
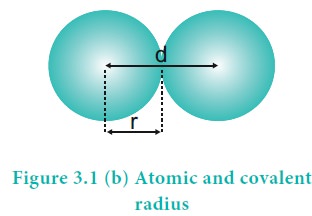
Covalent radius
It is one-half of the internuclear distance between two identical atoms linked together by a single covalent bond. Inter nuclear distance can be determined using x-ray diffraction studies.
Example:
The experimental internuclear distance in Cl2 molecule is 1.98 ├ģ. The covalent radius of chlorine is calculated as below.
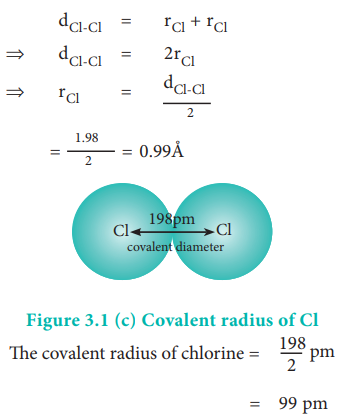
The formation of covalent bond involves the overlapping of atomic orbitals and it reduces the expected internuclear distance. Therefore covalent radius is always shorter than the actual atomic radius.
The covalent radius of individual atom can also be calculated using the internuclear distance (dA-B) between two different atoms A and B. The simplest method proposed by Schomaker and Stevenson is as follows.
dA-B = rA + rB - 0.09 (ŽćA-ŽćB)
where ŽćA and ŽćB are the electronegativities of A and B respectively in Pauling units
Here ŽćA ŽćB and radius is in ├ģ.
Let us calculate the covalent radius of hydrogen using the experimental d value is 1.28 ├ģ and the covalent radius of chlorine is 0.99 ├ģ. In pauling scale the electronegativity of chlorine and hydrogen are 3 and 2.1 respectively.
dH-Cl = rH + rCl - 0.09 ( ŽćCl - ŽćH)
1.28 = rH + 0.09 - 0.09 (3 - 2.1)
1.28 = rH + 0.09 - 0.09 (0.9)
1.28 = rH + 0.09 - 0.081
1.28 = rH + 0.909
Ōł┤ rH = 1.28 - 0.909 = 0.317 ├ģ
Metallic radius
It is defined as one-half of the distance between two adjacent metal atoms in the closely packed metallic crystal lattice.
For example, the distance between the adjacent copper atoms in solid copper is 2.56 ├ģ and therefore the metallic radius of copper is
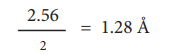
The metallic radius can be calculated using the unit cell length of the metallic crystal. You will study the detailed calculation procedure in XII standard solid state unit.
Periodic Trends in Atomic Radius
Variation in Periods
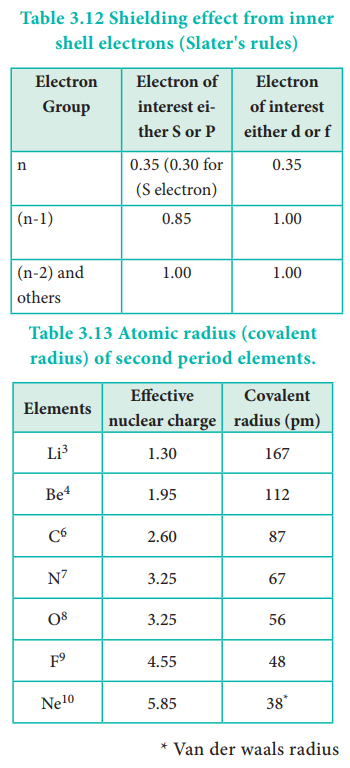
Atomic radius tends to decrease in a period. As we move from left to right along a period, the valence electrons are added to the same shell. The simultaneous addition of protons to the nucleus, increases the nuclear charge, as well as the electrostatic attractive force between the valence electrons and the nucleus. Therefore atomic radius decreases along a period.
Effective nuclear charge
In addition to the electrostatic forces of attraction between the nucleus and the electrons, there exists repulsive forces among the electrons. The repulsive force between the inner shell electrons and the valence electrons leads to a decrease in the electrostatic attractive forces acting on the valence electrons by the nucleus. Thus, the inner shell electrons act as a shield between the nucleus and the valence electrons. This effect is called shielding effect.
The net nuclear charge experienced by valence electrons in the outermost shell is called the effective nuclear charge. It is approximated by the below mentioned equation.
Zeff = Z ŌĆō S
Where Z is the atomic number and 'S' is the screening constant which can be calculated usi ng Slater's rules as described below.
Step 1 :
Write the electronic configuration of the atom and rearrange it by grouping ns and np orbitals together and others separately in the following form.
(1s) (2s, 2p) (3s, 3p) (3d) (4s, 4p) (4d) (4f) (5s, 5p)...
Step 2 :
Identify the group in which the electron of interest is present. The electron present right to this group does not contribute to the shielding effect.
Each of the electrons within the identified group (denoted by 'n') shields to an extent of 0.35 unit of nuclear charge. However, it is 0.30 unit for 1s electron.
Step 3 :
Shielding of inner shell electrons.
If the electron of interest belongs to either s or p orbital,
i) each electron within the (n-1) group shields to an extent of 0.85 unit of nuclear charge, and
ii) each electron within the (n-2) group (or) even lesser group (n-3, (n-4) etc...completely shields i.e. to an extent of 1.00 unit of nuclear charge.
If the electron of interest belongs to d or f orbital, then each of electron left of the group of electron of interest shields to an extent of 1.00 unit of nuclear charge.
Step 4 :
Summation of the shielding effect of all the electrons gives the shielding constant 'S'
Example: Let us explain the calculation of effective nuclear charge on 4s electron and 3d electron in scandium. The electronic configuration of scandium is 1s2, 2s2, 2p6, 3s 2, 3p6, 4s2, 3d1. we can rearrange as below.
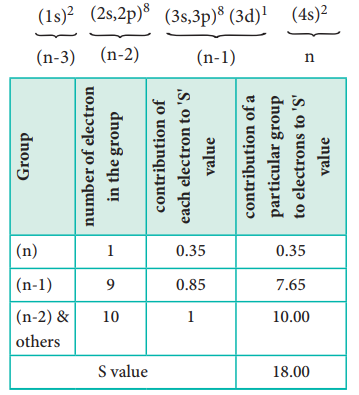
Zeff = Z ŌĆō S i.e.= 21- 18 Ōł┤Zeff = 3
Calculation of effective nuclear charge on 3d electron
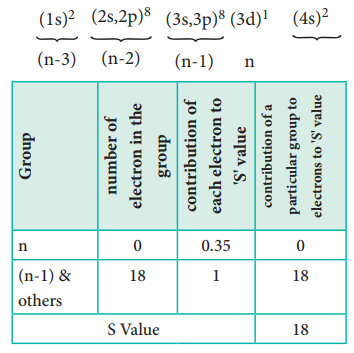
Ōł┤ Zeff = Z ŌĆō S i.e. =21 ŌĆō 18 Ōł┤ Zeff = 3
Variation in Group
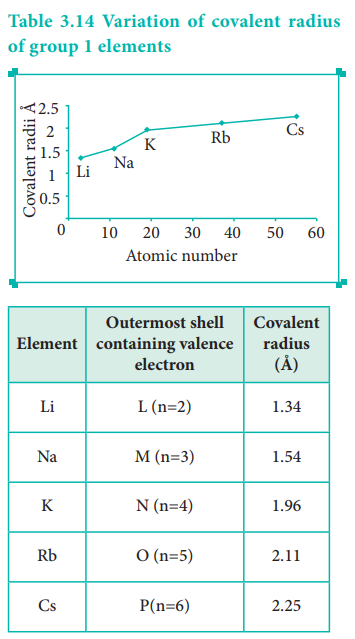
In the periodic table, the atomic radius of elements increases down the group. As we move down a group, new shells are opened to accommodate the newly added valence electrons. As a result, the distance between the centre of the nucleus and the outermost shell containing the valence electron increases. Hence, the atomic radius increases. The trend in the variation of the atomic radius of the alkali metals down the group os shown below.
Activity 3.1
Covalent radii (in ├ģ) for some elements of different groups and periods are listed below. Plot these values against atomic number. From the plot, explain the variation along a period and a group.
2nd group elements : Be (0.89), Mg (1.36), Ca (1.74), Sr (1.91) Ba(1.98)
17th group elements : F (0.72), Cl (0.99), Br (1.14), I (1.33)
3rd Period elements : Na(1.57), Mg(1.36), Al (1.25), Si(1.17), P(1.10), S(1.04), Cl(0.99)
4th period elements : K(2.03), Ca(1.74), Sc(1.44), Ti(1.32), V(1.22), Cr(1.17), Mn(1.17), Fe(1.17), Co(1.16), Ni(1.15), Cu(1.17), Zn(1.25), Ga(1.25), Ge(1.22), As(1.21), Se(1.14), Br(1.14)
Related Topics