statistical hypothesis: Null Hypothesis and Alternative Hypothesis, Level of Significants, Type of Errors

Meaning : Null Hypothesis and Alternative Hypothesis - Level of Significants and Type of Errors

Statistical Hypothesis

Statistical hypothesis is some assumption or statement, which may or may not be true, about a population.

There are two types of statistical hypothesis

(i) Null hypothesis  (ii) Alternative hypothesis

Null Hypothesis

Definition 8.7

According to Prof. R.A.Fisher, “Null hypothesis is the hypothesis which is tested for possible rejection under the assumption that it is true”, and it is denoted by H₀ .

For example: If we want to find the population mean has a specified value μ₀ , then the null hypothesis H₀  is set as follows H₀ : μ = μ₀

Alternative Hypothesis

Any hypothesis which is complementary to the null hypothesis is called as the alternative hypothesis and is usually denoted by H₁ .

For example: If we want to test the null hypothesis that the population has specified mean μ i.e., H₀ : μ = μ ₀ then the alternative hypothesis could be any one among the following:

i.            H₁ : μ ≠ μ ₀ (μ > or μ < μ ₀)

ii.            H₁ : μ > μ ₀

iii.            H₁ : μ < μ ₀

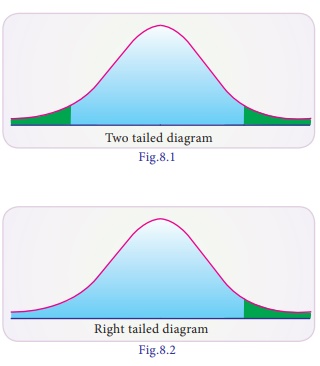
The alternative hypothesis in H₁ : μ ≠ μ ₀ is known as two tailed alternative test. Two tailed test is one where the hypothesis about the population parameter is rejected for the value of sample statistic falling into either tails of the sampling distribution. When the hypothesis about the population parameter is rejected only for the value of sample statistic falling into one of the tails of the sampling distribution, then it is known as one-tailed test. Here H₁ : μ > μ ₀ and H₁ : μ < μ₀ are known as one tailed alternative.

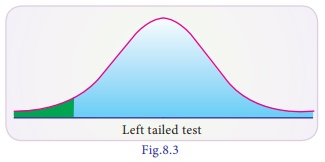
Right tailed test: H₁ : μ > μ ₀ is said to be right tailed test where the rejection region or critical region lies entirely on the right tail of the normal curve.

Left tailed test: H₁ : μ < μ ₀ is said to be left tailed test where the critical region lies entirely on the left tail of the normal curve. (diagram)

Types of Errors in Hypothesis testing

There is every chance that a decision regarding a null hypothesis may be correct or may not be correct. There are two types of errors. They are

Type I error: The error of rejecting H₀  when it is true.

Type II error: The error of accepting when H₀  it is false.

Critical region or Rejection region

A region corresponding to a test statistic in the sample space which tends to rejection of H₀ is called critical region or region of rejection.

Level of significance

The probability of type I error is known as level of significance and it is denoted by . The level of significance is usually employed in testing of hypothesis are 5% and 1%. The level of significance is always fixed in advance before collecting the sample information.

Critical values or significant values

The value of test statistic which separates the critical (or rejection) region and the acceptance region is called the critical value or significant value. It depend upon

(i) The level of significance

(ii) The alternative hypothesis whether it is two-tailed or single tailed.

For large samples, the standardized variable corresponding to the statistic  viz.,

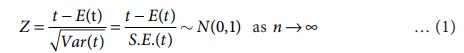
The value of Z given by (1) under the null hypothesis is known as test statistic. The critical values of Z at commonly used level of significance for both two tailed and single tailed tests are given in the normal probability table (Refer the normal probably Table).

Since for large n, almost all the distributions namely, Binomial, Poisson, etc., can be approximated very closely by a normal probability curve, we use the normal test of significance for large samples.