Types of Random sampling or Probability sampling

Random sampling or Probability sampling

Random sampling refers to selection of samples from the population in a random manner. A random sample is one where each and every item in the population has an equal chance of being selected.

“ Every member of a parent population has had equal chances of being included”.- Dr. Yates

“A random sample is a sample selected in such a way that every item in the population has an equal chance of being included”.-Harper

The following are different types of probability sampling:

(i) Simple random sampling

(ii) Stratified random sampling

(iii) Systematic sampling

(i) Simple random sampling

In this technique the samples are selected in such a way that each and every unit in the population has an equal and independent chance of being selected as a sample. Simple random sampling may be done, with or without replacement of the samples selected. In a simple random sampling with replacement there is a possibility of selecting the same sample any number of times. So, simple random sampling without replacement is followed.

Thus in simple random sampling from a population of N units, the probability of drawing any unit at the first draw is 1/N , the probability of drawing any unit in the second draw from among the available (N-1) units is  1/(N-1). and so on. . Several methods have been adopted for random selection of the samples from the population. Of those, the following two methods are generally used and which are described below.

(A)  Lottery method

This is the most popular and simplest method when the population is finite. In this method, all the items of the population are numbered on separate slips of paper of same size, shape and colour. They are folded and placed in a container and shuffled thoroughly. Then the required numbers of slips are selected for the desired sample size. The selection of items thus depends on chance.

For example, if we want to select 10 students, out of 100 students, then we must write the names/roll number of all the 100 students on slips of the same size and mix them, then we make a blindfold selection of 10 students. This method is called unrestricted random sampling, because units are selected from the population without any restriction. This method is mostly used in lottery draws. If the population or universe is infinite, this method is inapplicable.

(B)     Table of Random number

When the population size is large, it is difficult to number all the items on separate slips of paper of same size, shape and colour. The alternative method is that of using the table of random numbers. The most practical, easy and inexpensive method of selecting a random sample can be done through “Random Number Table”. The random number table has been so constructed that each of the digits 0,1,2,…,9 will appear approximately with the same frequency and independently of each other.

The various random number tables available are

a. L.H.C. Tippett random number series

b. Fisher and Yates random number series

c. Kendall and Smith random number series

d. Rand Corporation random number series.

Tippett’s table of random numbers is most popularly used in practice. Given below the first forty sets from Tippett’s table as an illustration of the general appearance of random numbers:

Suppose, if we want to select the required number of samples from a population of size N(<99) then any two digit random number can be selected from ( 00 to 99) from the above random number table. Similarly if N(< 999) or (< 9999), then any three digit random number or four digit random number can be selected from (000 to 999) or (0000 to 9999).

The procedure of selecting the random samples consists of following steps:

1. Identify the N units in the population with the numbers from 1 to N.

2. Select at random, any page from the ‘Random Number Table’.

3. Select the required number of samples from any row or column or diagonal.

One may question, as to how it is ensured that these digits are random. It may be pointed out that the digits in the table were chosen horizontally but the real guarantee of their randomness lies in practical tests. Tippett’s numbers have been subjected to numerous tests and used in many investigations and their randomness has been very well established for all practical purposes.

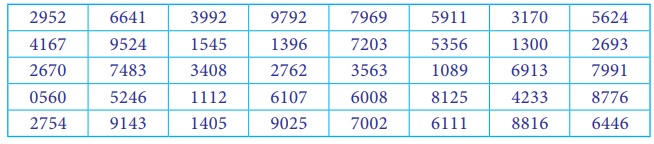
An example to illustrate how Tippett’s table of random numbers may be used is given below. Suppose we have to select 20 items out of 6,000. The procedure is to number all the 6,000 items from 1 to 6,000. A page from Tippett’s table may be selected and the first twenty numbers ranging from 1 to 6,000 are noted down. If the numbers are above 6000, choose the next number ranging from 1 to 6000. Items bearing those numbers will be selected as samples from the population. Making use of the portion of the random number table given,the requiredrandom samples are shaded. Here, we consider row wise selection of random numbers.

If the population size is 1,000 and suppose we want to select 15 items out of 1,000. All itemsfrom 1 to 1000 should be numbered as 0001 to 1000.Now, we may now select 15 numbers from the random number table.The procedure will be different, as Tippett’s random numbers are available only in four digits. Thus, we can select the first three digits from the four digit random sample number.Making use of the portion of the random number table given, the required random samples are shaded in RED colour. Here, we consider row wise selection of random numbers.

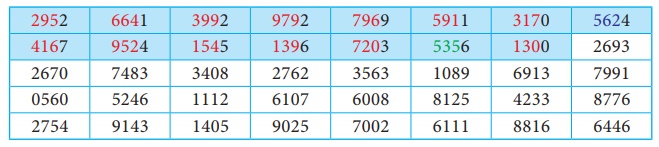
If the population size is 100 and suppose we want to select 10 items out of 100. All itemsfrom 1 to 100 should be numbered as 001 to 100.Now, we may now select 10 numbers from the random number table. The procedure will be different, as Tippett’s random numbers are available only in four digits. Thus, we can select the first two digits from the four digit random sample number. Making use of the portion of the random number table given, the required random samples are shaded in RED colour.Here, we consider row wise selection of random numbers.

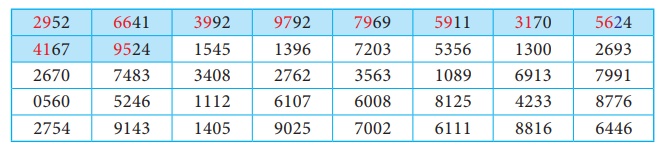
Merits and demerits of Simple Random Sampling:

Merits

1. Personal bias is completely eliminated.

2. This method is economical as it saves time, money and labour.

3. The method requires minimum knowledge about the population in advance.

Demerits

1. This requires a complete list of the population but such up-to-date lists are not available in many enquiries.

2. If the size of the sample is small, then it will not be a representative of the population.

Example 8.1

Using the Kendall-Babington Smith - Random number table,Draw5 random samples.

Solution:

There many ways to select 5random samples from the given Kendall-Babington Smith - Random number table. Assume that at random we select 3rd column 1stvalue. This location gives the digit to be 75. So the first sample will be 75, and then the next choices can be in the same 3rd column which follows as 55, 16, 67 and 26. Therefore 75, 55,16,67 and 26 will be used as random samples. The various shaded numbers can be taken as 5 random sample numbers. Apart from this, one can select any 5 random sample numbers as they like.

Example 8.2

Using the following Tippett’s random number table,

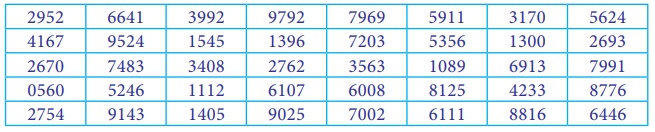
Draw a sample of 15 houses from Cauvery Street which has 83 houses in total.

Solution:

There many ways to select 15 random samples from the given Tippet’s random number table. Since the population size is 83(two-digit number). Here the door numbers are assigned from 1 to 83. Assume that at random we first choose 2nd column. So the first sample is 66 and other 14 samples are 74, 52, 39, 15, 34, 11, 14, 13, 27, 61, 79, 72, 35, and 60. If the numbers are above 83, choose the next number ranging from 1 to 83.

Example 8.3

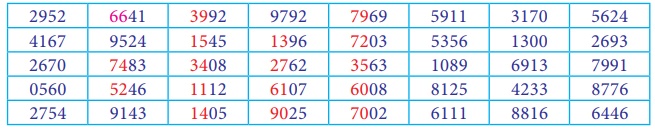
Using the following random number table,

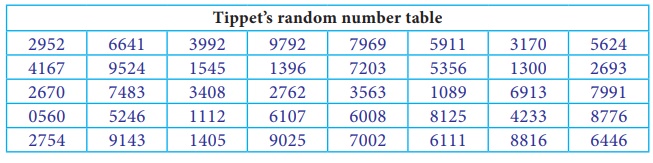
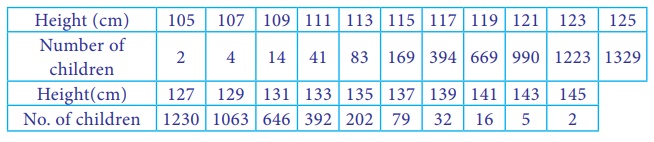
Draw a sample of 10 children with theirheight from the population of 8,585 children as classified hereunder.

Solution:

The first thing is to number the population(8585 children). The numbering has already been provided by the frequency table. There are 2 children with height of 105 cm, therefore we assign number 1 and 2 to the children those in the group 105 cm, number 3 to 6 is assigned to those in the group 107 cm and similarly all other children are assigned the numbers. In the last group 145 cms there are two children with assigned number 8584 and 8585.

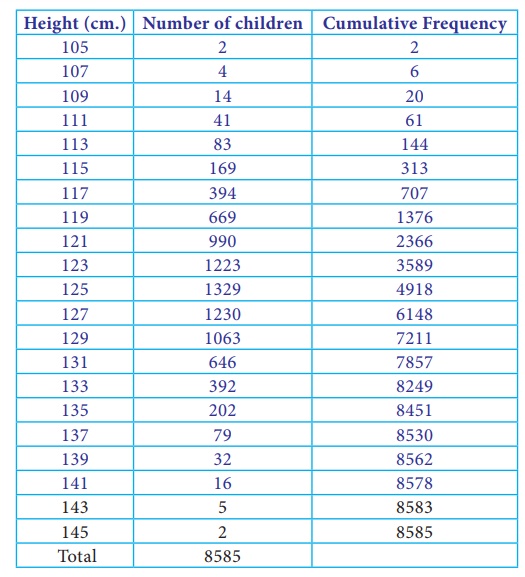
Now we take 10 samples from the tables, since the population size is in 4 digits we can use the given random number table. Select the10 random numbers from 1 to 8585 in the table, Here, we consider column wise selection of random numbers, starting from first column.

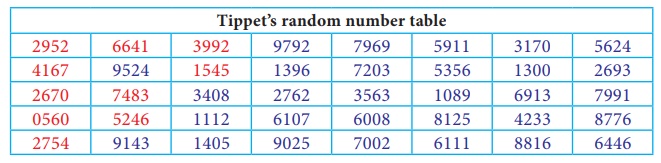
The children with assigned number 2952 is selected and then see the cumulative frequency table where 2952 is present, now select the corresponding row height which is 123 cm, similarly all the selected random numbers are considered for the selection of the child with their corresponding height. The following table shows all the selected 10 children with their heights.

Example 8.4

Using the following random number table (Kendall-Babington Smith)

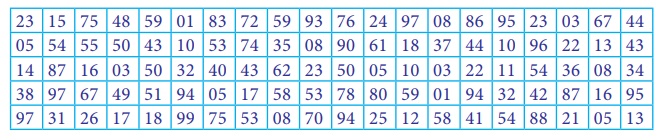
Draw a random sample of 10 four- figure numbers startingfrom 1550 to 8000.

Solution:

Here, we have to select 10 random numbers ranging from 1550 to 8000 but the given random number table has only 2 digit numbers. To solve this, two - 2 digit numbers can be combined together to make a four- figure number. Let us select the 5thand 6th column and combine them to form a random number, then select the random number with given range. This gives 5random numbers, similarly 8th and 9th is selected and combined to form a random numbers, then select the random number with given range. This gives 5random numbers, totally 10 four- figure numbers have been selected. The following table shows the 10 random numbers which are combined and selected.

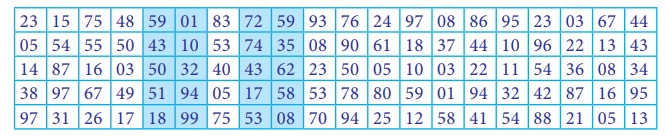
Therefore the selected 10 random numbers are

(ii) Stratified Random Sampling

Definition 8.1

In stratified random sampling, first divide the population into sub-populations, which are called strata. Then, the samples are selected from each of the strata through random techniques.The collection of all the samples from all strata gives the stratified random samples.

When the population is heterogeneous or different segments or groups with respect to the variable or characteristic under study, then Stratified Random Sampling method is studied. First, the population is divided into homogeneous number of sub-groups or strata before the sample is drawn. A sample is drawn from each stratum at random. Following steps are involved for selecting a random sample in a stratified random sampling method.

(a) The population is divided into different classes so that each stratum will consist of more or less homogeneous elements. The strata are so designed that they do not overlap each other.

(b) After the population is stratified, a sample of a specified size is drawn at random from each stratum using Lottery Method or Table of Random Number Method.

Stratified random sampling is applied in the field of the different legislative areas as strata in election polling, division of districts (strata) in a state etc…

Example 8.5

From the following data, select 68 random samples from the populationof heterogeneous group with size of 500 through stratified random sampling, considering the following categories as strata.

Category1: Lower income class -39%

Category2: Middle income class - 38%

Category3: Upper income class- 23%

Solution

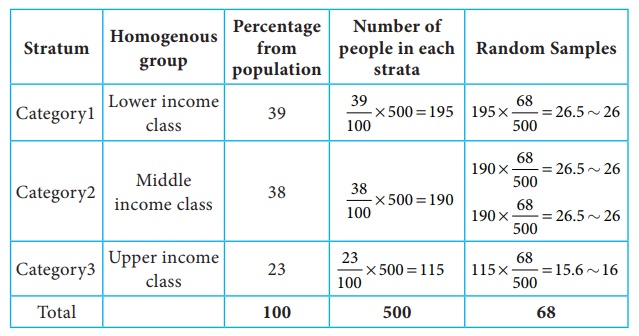
Merits

(a) A random stratified sample is superior to a simple random sample because it ensures representation of all groups and thus it is more representative of the population which is being sampled.

(b) A stratified random sample can be kept small in size without losing its accuracy.

(c) It is easy to administer,if the population under study is sub-divided.

(d) It reduces the time and expenses in dividing the strata into geographical divisions, since the government itself had divided the geographical areas. 

Demerits

(a) To divide the population into homogeneous strata (if not divided), it requires more money, time and statistical experience which is a difficult one.

(b) If proper stratification is not done, the sample will have an effect of bias.

(c) There is always a possibility of faulty classification of strata and hence increases variability.

(iii) Systematic Sampling

Definition 8.2

In a systematic sampling, randomly select the first sample from the first k units.

Then every k th member, starting with the first selected sample, is included in the sample.

Systematic sampling is a commonly used technique, if the complete and up-to-date list of the sampling units is available. We can arrange the items in numerical, alphabetical, geographical or in any other order. The procedure of selecting the samples starts with selecting the first sample at random, the rest being automatically selected according to some pre-determined pattern. A systematic sample is formed by selecting every item from the population, where k refers to the sample interval. The sampling interval can be determined by dividing the size of the population by the size of the sample to be chosen.

That is k = N/n ,where k is an integer.

k = Sampling interval , Size of the population, Sample size. Procedure for selection of samples by systematic sampling method

(i) If we want to select a sample of 10 students from a class of 100 students, the sampling interval is calculated as k = N/n = 100/10 =10 .

Thus sampling interval = 10 denotes that for every 10 samples one sample has to be selected.

(ii) The firstsample is selected from the first 10 (sampling interval) samples through random selection procedures.

(iii) If the selected first random sample is 5, then the rest of the samples are automatically selected by incrementing the value of the sampling interval (k = 10) i.e., 5, 15 , 25, 35, 45, 55, 65, 75, 85, 95.

Example:

Suppose we have to select 20 items out of 6,000. The procedure is to number all the 6,000 items from 1 to 6,000. The sampling interval is calculated as k = N/n = 6000/20 = 300.

Thus sampling interval = 300 denotes that for every 300 samples one sample has to be selected. The first sample is selected from the first 300 (sampling interval) samples through random selection procedures. If the selected first random sample is 50, then the rest of the samples are automatically selected by incrementing the value of the sampling interval (k=300) ie,50, 350, 650, 950, 1250, 1550, 1850, 2150, 2450, 2750, 3050, 3350, 3650, 3950, 4250, 4550, 4850, 5150, 5450, 5750. Items bearing those numbers will be selected as samples from the population.

Merits

1. This is simple and convenient method.

2. This method distributes the sample more evenly over the entire listed population.

3. The time and work is reduced much.

Demerits

1. Systematic samples are not random samples.

2. If N is not a multiple of n, then the sampling interval (k) cannot be an integer, thus sample selection becomes difficult.