Sampling distribution

Sampling distribution

Definition 8.3

Sampling distribution of a statistic is the frequency distribution which is formed with various values of a statistic computed from different samples of the same size drawn from the same population.

For instance if we draw a sample of size n from a given finite population of size N, then the total number of possible samples is 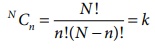 For each of these k samples we can compute some statistic, t = t(x₁ , x₂ , x ₃ ,...x_n ), in particular the mean  , the variance S2, etc., is given below

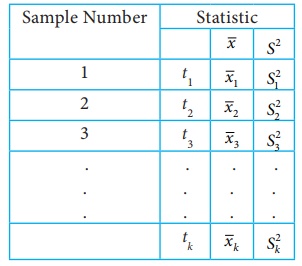
The set of the values of the statistic so obtained, one for each sample, constitutes the sampling distribution of the statistic.

Standard Error

The standard deviation of the sampling distribution of a statistic is known as its Standard Error abbreviated as S.E. The Standard Errors (S.E.) of some of the well-known statistics, for large samples, are given below, where n is the sample size, σ² is the population variance.