Estimation

Estimation:

It is possible to draw valid conclusion about the population parameters from sampling distribution. Estimation helps in estimating an unknown population parameter such as population mean, standard deviation, etc., on the basis of suitable statistic computed from the samples drawn from population.

Estimation:

Definition 8.4

The method of obtaining the most likely value of the population parameter using statistic is called estimation.

Estimator:

Definition 8.5

Any sample statistic which is used to estimate an unknown population parameter is called an estimator ie., an estimator is a sample statistic used to estimate a population parameter.

Estimate:

Definition 8.6

When we observe a specific numerical value of our estimator, we call that value is an estimate. In other words, an estimate is a specific observed value of a statistic.

Characteristic of a good estimator

A good estimator must possess the following characteristic:

(i) Unbiasedness

(ii) Consistency

(iii) Efficiency

(iv) Sufficiency.

i. Unbiasedness: An estimator T_n =T(x₁ , x₂ ,...., x_n ) is said to be an unbiased estimator of γ (θ ) if E (T_n ) = γ (θ) , for all θ ε θ (parameter space), (i.e)An estimator is said to be unbiased if its expected value is equal to the population parameter. Example: E () = μ

ii. Consistency: An estimator T_n =T(x₁ , x₂ ,...., x_n ) is said to be consistent estimator of γ (θ ) if T_n converges to γ θ( ) in Probability, i.e., 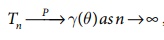 for all θ ε Ѳ .

iii. Efficiency:If T₁ is the most efficient estimator with variance V₁ and T₂ is any other estimator with variance V₂ , then the efficiency E of T₂ is defined as E=V₁/V₂. Obviously, E cannot exceed unity.

iv.  Sufficiency: If T = t(x₁ , x₂ ,...., x_n ) is an estimator of a parameter θ , based on a sample  x₁ , x₂ ,...., x_n of size n from the population with density  f (x, θ) such that the conditional distribution of x₁ , x₂ ,...., x_n  given T , is independent of q , then T is sufficient estimator for θ.