Hypothesis Testing: Solved Example Problems

Example 8.14

An auto company decided to introduce a new six cylinder car whose mean petrol consumption is claimed to be lower than that of the existing auto engine. It was found that the mean petrol consumption for the 50 cars was 10 km per litre with a standard deviation of 3.5 km per litre. Test at 5% level of significance, whether the claim of the new car petrol consumption is 9.5 km per litre on the average is acceptable.

Solution:

Sample size n =50 Sample mean  = 10 km Sample standard deviation s = 3.5 km

Population mean μ = 9.5 km

Since population SD is unknown we consider σ = s

The sample is a large sample and so we apply Z-test

Null Hypothesis: There is no significant difference between the sample average and the company’s claim, i.e., H₀ : μ = 9.5

Alternative Hypothesis: There is significant difference between the sample average and the company’s claim, i.e., H₁ : μ ≠ 9.5 (two tailed test)

The level of significance α = 5% = 0.05

Applying the test statistic

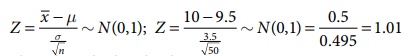
Thus the calculated value 1.01 and the significant value or table value Z_α/2 = 1.96

Comparing the calculated and table value ,Here Z < Z_α/2 i.e., 1.01<1.96.

Inference:Since the calculated value is less than table value i.e., Z < Z_α/2 at 5% level of sinificance, the null hypothesis H₀ is accepted. Hence we conclude that the company’s claim that the new car petrol consumption is 9.5 km per litre is acceptable.

Example 8.15

A manufacturer of ball pens claims that a certain pen he manufactures has a mean writing life of 400 pages with a standard deviation of 20 pages. A purchasing agent selects a sample of 100 pens and puts them for test. The mean writing life for the sample was 390 pages. Should the purchasing agent reject the manufactures claim at 1% level?

Solution:

Sample size n =100, Sample mean  = 390 pages, Population mean μ = 400 pages

Population SD σ = 20 pages

The sample is a large sample and so we apply Z -test

Null Hypothesis: There is no significant difference between the sample mean and the population mean of writing life of pen he manufactures, i.e., H₀ : μ = 400

Alternative Hypothesis: There is significant difference between the sample mean and the population mean of writing life of pen he manufactures, i.e., H₁ : μ ≠ 400 (two tailed test)

The level of significance a = 1% = 0.01

Applying the test statistic

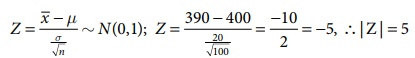
Thus the calculated value |Z| = 5 and the significant value or table value Z_α/2 = 2.58

Comparing the calculated and table values, we found Z > Z_α/2 i.e., 5 > 2.58

Inference: Since the calculated value is greater than table value i.e., Z > Z_α/2 at 1% level of significance, the null hypothesis is rejected and Therefore we concluded that μ ≠ 400 and the manufacturer’s claim is rejected at 1% level of significance.

Example 8.16

(i) A sample of 900 members has a mean 3.4 cm and SD 2.61 cm. Is the sample taken from a large population with mean 3.25 cm. and SD 2.62 cm?

(ii) If the population is normal and its mean is unknown, find the 95% and 98% confidence limits of true mean.

Solution:

(i) Given:

Sample size n = 900, Sample mean  = 3.4 cm, Sample SD σ = 2.61 cm

Population mean μ= 3.25 cm, Population SD σ = 2.61 cm

Null Hypothesis H₀ : μ = 3.25 cm (the sample has been drawn from the population mean

μ = 3.25 cm and SD σ = 2.61 cm)

Alternative Hypothesis H₁ : μ ≠ 3.25 cm (two tail) i.e., the sample has not been drawn from the population mean μ = 3.25 cm and SD σ = 2.61 cm.

The level of significance α = 5% = 0.05

Teststatistic:

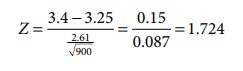
∴ Z = 1.724

Thus the calculated and the significant value or table value Z_α/2 = 1.96

Comparing the calculated and table values, Z < Z_α/2 i.e., 1.724 < 1.96

Inference:Since the calculated value is less than table value i.e., Z > Z_α/2 at 5% level of significance, the null hypothesis is accepted. Hence we conclude that the2 data doesn’t provide us any evidence against the null hypothesis. Therefore, the sample has been drawn from the population mean μ = 3.25 cm and SD, σ = 2.61 cm.

(ii) Confidence limits

95% confidential limits for the population mean μ are :

 – Z_α/2 SE ≤ µ ≤  + Z_α/2 SE

3.4− (1.96× 0.087)≤ μ ≤ 3.4+ (1.96× 0.087)

3.229≤ μ ≤ 3.571

98% confidential limits for the population mean are :

 − Zα/2 SE ≤ µ ≤  + Z_α/2 SE

3.4− (2.33× 0.087)≤ μ ≤ 3.4+ (2.33× 0.087)

3.197 ≤ μ≤ 3.603

Therefore,95% confidential limits is (3.229,3.571) and 98% confidential limits is (3.197,3.603).

Example 8.17

The mean weekly sales of soap bars in departmental stores were 146.3 bars per store. After an advertising campaign the mean weekly sales in 400 stores for a typical week increased to 153.7 and showed a standard deviation of 17.2. Was the advertising campaign successful?

Solution:

Sample size n = 400 stores

Sample mean  = 153.7 bars

Sample SD s = 17.2 bars

Population mean μ = 146.3 bars

Since population SD is unknown we can consider the sample SD s = σ

Null Hypothesis. The advertising campaign is not successful i.e, H₀ : μ = 146.3 (There is no significant difference between the mean weekly sales of soap bars in department stores before and after advertising campaign)

Alternative Hypothesis H₁ : μ > 143.3 (Right tail test). The advertising campaign was successful

Level of significance a = 0.05

Test statistic

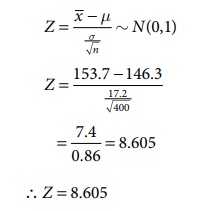
∴ Z = 8.605

Comparing the calculated value Z = 8.605 and the significant value or table value Zα = 1.645 . we get 8.605 > 1.645

Inference: Since, the calculated value is much greater than table value i.e., Z > Zα , it is highly significant at 5% level of significance. Hence we reject the null hypothesis H0 and conclude that the advertising campaign was definitely successful in promoting sales.

Example 8.18

The wages of the factory workers are assumed to be normally distributed with mean and variance 25. A random sample of 50 workers gives the total wages equal to ₹ 2,550. Test the hypothesis μ = 52, against the alternative hypothesis μ = 49 at 1% level of significance.

Solution:

Sample size n = 50 workers

Since alternative hypothesis is of two tailed test we can take | Z | = 1.4142

Critical value at 1% level of significance is Z_α/2 = 2.58

Inference: Since the calculated value is less than table value i.e., Z < Za at 1% level of significance, the null hypothesis H₀ is accepted. Therefore, we conclude 2that there is no significant difference between the sample mean and population mean μ= 52 and SD σ = 5.

Example 8.19

An ambulance service claims that it takes on the average 8.9 minutes to reach its destination in emergency calls. To check on this claim, the agency which licenses ambulance services has them timed on 50 emergency calls, getting a mean of 9.3 minutes with a standard deviation of 1.6 minutes. What can they conclude at the level of significance.

Solution:

Calculated value Z = 1.7676

Critical value at 5% level of significance is Z_α/2 = 1.96

Inference: Since the calculated value is less than table value i.e., Z < Z_α/2 at 5% level of significance, the null hypothesis is accepted. Therefore we conclude that an ambulance service claims on the average 8.9 minutes to reach its destination in emergency calls.