Testing Procedure : Large sample theory and test of significants for single mean

Testing Procedure : Large sample theory and test of significants for single mean

The following are the steps involved in hypothesis testing problems

1. Null hypothesis: Set up the null hypothesis H₀

2. Alternative hypothesis: Set up the alternative hypothesis . This will enable us to decide whether we have to use two tailed test or single tailed test (right or left tailed)

3. Level of significance: Choose the appropriate level of significant (a) depending on the reliability of the estimates and permissible risk. This is to be fixed before sample is drawn. i.e., a is fixed in advance.

4. Test statistic : Compute the test statistic

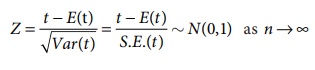
5. Conclusion: We compare the computed value of Z in step 4 with the significant value or critical value or table value Z_a at the given level of significance .

i.            If | Z |< Za  i.e., if the calculated value of is less than critical value we say it is not significant. This may due to fluctuations of sampling and sample data do not provide us sufficient evidence against the null hypothesis which may therefore be accepted.

ii.            If | Z |> Z_a i.e., if the calculated value of is greater than critical value Z_a  then we say it is significant and the null hypothesis is rejected at level of significance α.

Test of significance for single mean

Let x_i , (i = 1,2,3,...,n) is a random sample of size from a normal population with mean μ and variance σ² then the sample mean is distributed normally with mean and variance σ²/n, .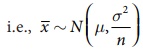

Thus for large samples, the standard normal variate corresponding to  is :

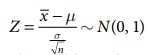
Under the null hypothesis that the sample has been drawn from a population with mean and variance σ² , i.e., there is no significant difference between the sample mean () and the population mean (α) , the test statistic (for large samples) is:

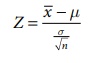
Remark:

If the population standard deviation s is unknown then we use its estimate provided by the sample variance given by σˆ² = s₂ = >  σˆ = s