Example Solved Problems with Answer, Solution | Sampling and Non-Sampling Errors - Computing standard error in simple cases | 12th Business Maths and Statistics : Chapter 8 : Sampling Techniques and Statistical Inference
Chapter: 12th Business Maths and Statistics : Chapter 8 : Sampling Techniques and Statistical Inference
Computing standard error in simple cases
Computing
standard error in simple cases
Example 8.6
A server channel
monitored for an hour was found to have an estimated mean of 20 transactions
transmitted per minute. The variance is known to be 4. Find the standard error.
Solution:
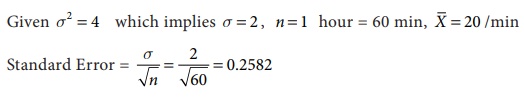
Example 8.7
Find the sample size for
the given standard deviation 10 and the standard error with respect of sample
mean is 3.
Solution:

Example 8.8
A die is thrown 9000
times and a throw of 3 or 4 is observed 3240 times. Find the standard error of
the proportion for an unbiased die .
Solution:
If the occurrence of 3
or 4 on the die is called a success, then
Sample size = 9000;
Number of Success = 3240
Sample proportion = p =
3240/9000 = 0 36.
Population proportion
(P) = Prob(getting 3 or 4 when a die is thrown)
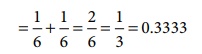
Thus P = 0.3333 and Q =
1–P=1– 0.3333 = 0.6667
The S.E for sample
proportion is given by

Hence the standard error for sample proportion is S.E=0.00496.
Example 8.9
The standard deviation
of a sample of size 50 is 6.3. Determine the standard error whose population
standard deviation is 6?
Solution:

Example 8.10
A sample of 100 students
is chosen from a large group of students. The average height of these students
is 162 cm and standard deviation (S.D) is 8 cm. Obtain the standard error for
the average height of large group of students of 160 cm?
Solution:
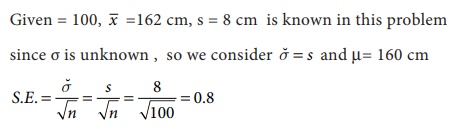
Therefore the standard error for the
average height of large group of students of 160 cm is 0.8.
Related Topics