Chapter: Digital Signal Processing : Signals and System
Z Tranform - Analysis of LTI System
ANALYSIS OF LTI SYSTEM
Z TRANFORM
INTRODUCTION TO Z TRANSFORM
For analysis of continuous time LTI system Laplace transform is used. And for analysis of discrete time LTI system z transform is used. Z transform is mathematical tool used for conversion of time domain into frequency domain (z domain) and is a function of the complex valued variable Z. The z transform of a discrete time signal x(n) denoted by
X(z) and given as

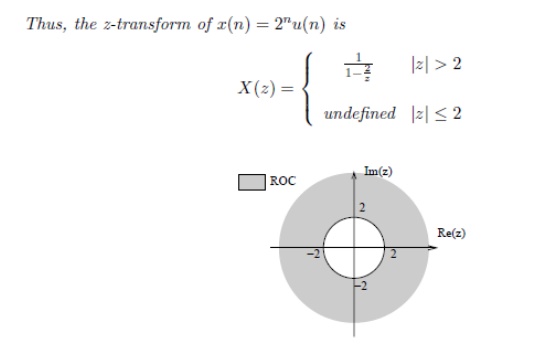
Z transform is an infinite power series because summation index varies from -∞ to ∞. But it is useful for values of z for which sum is finite. The values of z for which f (z) is finite and lie within the region called as “region of convergence (ROC).
ADVANTAGES OF Z TRANSFORM
1. The DFT can be determined by evaluating z transform.
2. Z transform is widely used for analysis and synthesis of digital filter.
3. Z transform is used for linear filtering. z transform is also used for finding Linear convolution, cross-correlation and auto-correlations of sequences.
4. In z transform user can characterize LTI system (stable/unstable, causal/anti-causal) and its response to various signals by placements of pole and zero plot.
ADVANTAGES OF ROC(REGION OF CONVERGENCE)
1. ROC is going to decide whether system is stable or unstable.
2. ROC decides the type of sequences causal or anti-causal.
3. ROC also decides finite or infinite duration sequences.
Z TRANSFORM PLOT
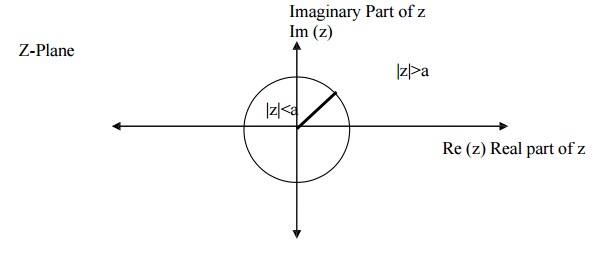
Fig show the plot of z transforms. The z transform has real and imaginary parts. Thus a plot of imaginary part versus real part is called complex z-plane. The radius of circle is 1 called as unit circle. This complex z plane is used to show ROC, poles and zeros. Complex variable z is also expressed in polar form as Z= rejω where r is radius of circle is given by |z| and ω is the frequency of the sequence in radians and given by ∟z.
Q) Determine z transform of following signals. Also draw ROC. i) x(n)= {1,2,3,4,5}
ii) x(n)={1,2,3,4,5,0,7}
Q) Determine z transform and ROC for x(n) = (-1/3)n u(n) –(1/2)n u(-n-1). Q)
Determine z transform and ROC for x(n) = [ 3.(4n)–4(2n)] u(n).
Q) Determine z transform and ROC for x(n) = (1/2)n u(-n).
Q) Determine z transform and ROC for x(n) = (1/2)n {u(n) – u(n-10)}.
Q) Find linear convolution using z transform. X(n)={1,2,3} & h(n)={1,2}
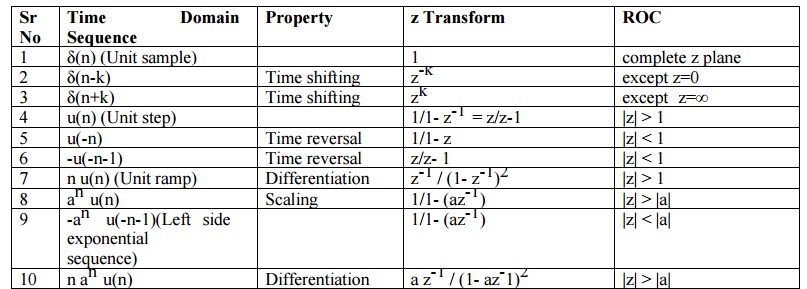
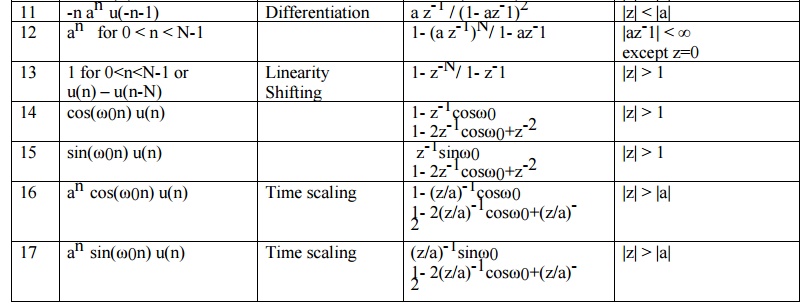
PROPERTIES OF Z TRANSFORM (ZT)
1) Linearity
The linearity property states that if z
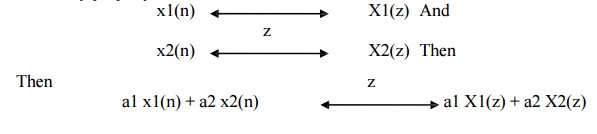
z Transform of linear combination of two or more signals is equal to the same linear combination of z transform of individual signals.
2) Time shifting
The Time shifting property states that if z x(n)

Thus shifting the sequence circularly by „k samples is equivalent to multiplying its z transform by z –k
3) Scaling in z domain
This property states that if

Thus scaling in z transform is equivalent to multiplying by an in time domain.
4) Time reversal Property
The Time reversal property states that if z

It means that if the sequence is folded it is equivalent to replacing z by z-1 in z domain.
5) Differentiation in z domain
The Differentiation property states that if z

6) Convolution Theorem
The Circular property states that if z
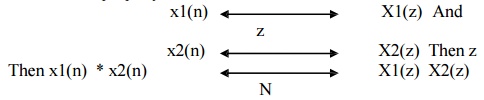
Convolution of two sequences in time domain corresponds to multiplication of its Z transform sequence in frequency domain.
7) Correlation Property
The Correlation of two sequences states that if z
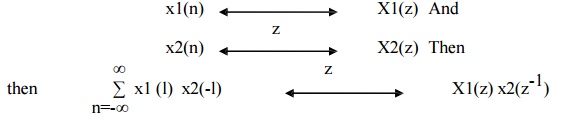
8) Initial value Theorem
Initial value theorem states that if z

9) Final value Theorem
Final value theorem states that if z
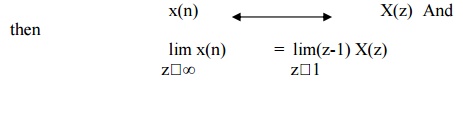
RELATIONSHIP BETWEEN FOURIER TRANSFORM AND Z TRANSFORM.
There is a close relationship between Z transform and Fourier transform. If we replace the complex variable z by e –jω, then z transform is reduced to Fourier transform.
Z transform of sequence x(n) is given by

Fourier transform of sequence x(n) is given by

Complex variable z is expressed in polar form as Z= rejω where r= |z| and ω is ∟z. Thus we can be written as
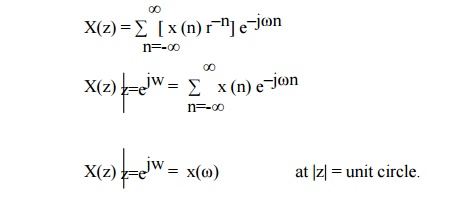
Thus, X(z) can be interpreted as Fourier Transform of signal sequence (x(n) r–n). Here r–n grows with n if r<1 and decays with n if r>1. X(z) converges for |r|= 1. hence Fourier transform may be viewed as Z transform of the sequence evaluated on unit circle. Thus The relationship between DFT and Z transform is given by
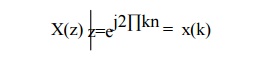
The frequency ω=0 is along the positive Re(z) axis and the frequency ∏/2 is along the positive Im(z) axis. Frequency ∏ is along the negative Re(z) axis and 3∏/2 is along the negative Im(z) axis.
INVERSE Z TRANSFORM (IZT)
The signal can be converted from time domain into z domain with the help of z transform (ZT). Similar way the signal can be converted from z domain to time domain with the help of inverse z transform(IZT). The inverse z transform can be obtained by using two different methods.
1) Partial fraction expansion Method (PFE) / Application of residue theorem
2) Power series expansion Method (PSE)
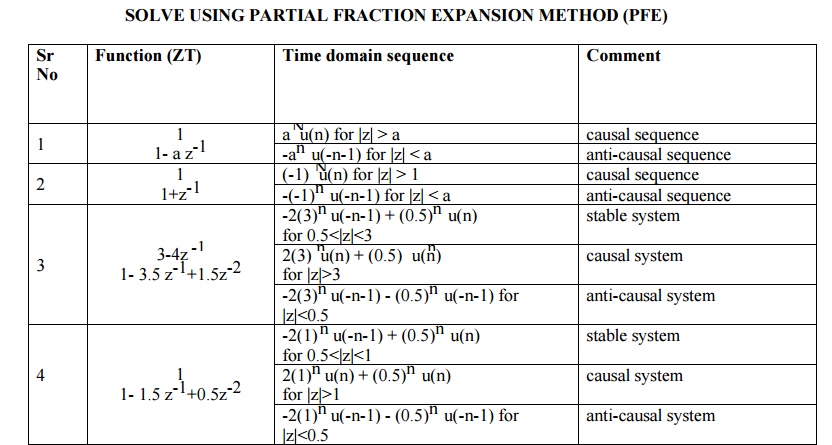
1. PARTIAL FRACTION EXPANSION METHOD
In this method X(z) is first expanded into sum of simple partial fraction.

The above equation can be written in partial fraction expansion form and find the coefficient AK and take IZT.

2. RESIDUE THEOREM METHOD
In this method, first find G(z)= zn-1 X(Z) and find the residue of G(z) at various poles of X(z).

3. POWER-SERIES EXPANSION METHOD
The z transform of a discrete time signal x(n) is given as
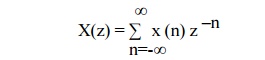
Expanding the above terms we have
x(z) = …..+x(-2)Z2+ x(-1)Z+ x(0)+ x(1) Z-1 + x(2) Z2 +….. (2)
This is the expansion of z transform in power series form. Thus sequence x(n) is given as
x(n) ={ ….. ,x(-2),x(-1),x(0),x(1),x(2),…………..}.
Power series can be obtained directly or by long division method.
SOLVE USING “POWER SERIES EXPANSION“ METHOD

RECURSIVE ALGORITHM

Thus
X(0) = a0/b0
X(1) = 1/b0 [ a1- x(0) b1]
X(2) = 1/b0 [ a1- x(1) b1 - x(0) b2] ……………
SOLVE USING “RECURSIVE ALGORITHM“ METHOD

Example 2:Find the magnitude and phase plot of

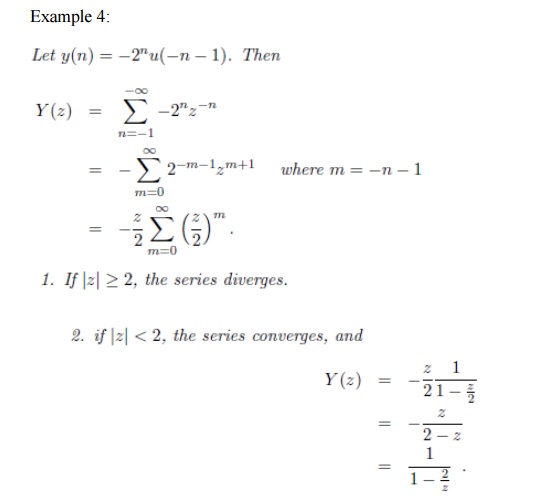
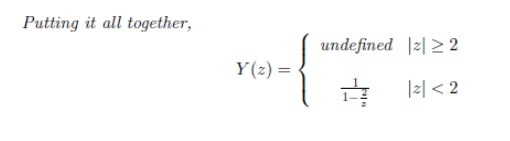
Example 5:Find the inverse Z Transform

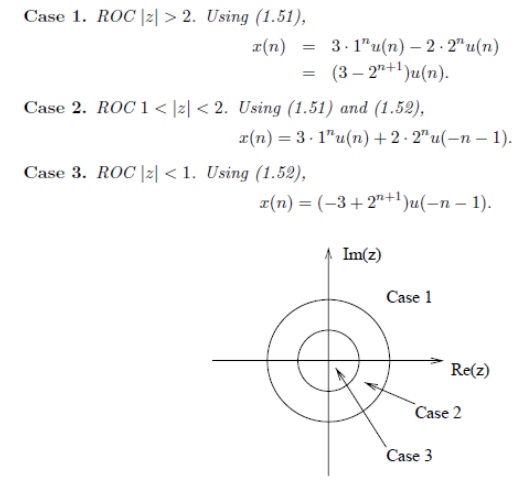
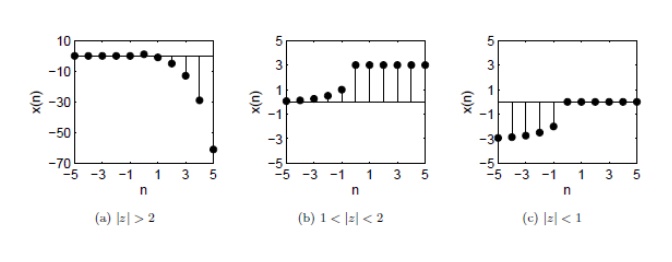
POLE –ZERO PLOT
X(z) is a rational function, that is a ratio of two polynomials in z-1 or z.
The roots of the denominator or the value of z for which X(z) becomes infinite, defines locations of the poles. The roots of the numerator or the value of z forwhich X(z) becomes zero, defines locations of the zeros.
ROC dos not contain any poles of X(z). This is because x(z) becomes infinite at the locations of the poles. Only poles affect the causality and stability of the system.
CASUALTY CRITERIA FOR LSI SYSTEM
LSI system is causal if and only if the ROC the system function is exterior to
the circle. i. e |z| > r. This is the condition for causality of the LSI system in terms of z transform. (The condition for LSI system to be causal is h(n) = 0 ….. n<0 )
STABILITY CRITERIA FOR LSI SYSTEM
Bounded input x(n) produces bounded output y(n) in the LSI system only if
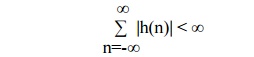
With this condition satisfied, the system will be stable. The above equation states that the LSI system is stable if its unit sample response is absolutely summable. This is necessary and sufficient condition for the stability of LSI system.

Magnitudes of overall sum is less than the sum of magnitudes of individual sums.
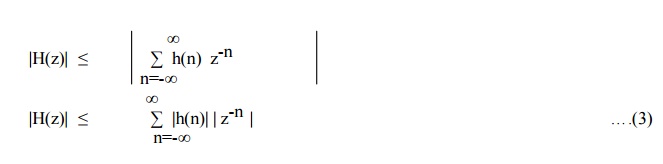
If H(z) is evaluated on the unit circle | z-n|=|z|=1.
Hence LSI system is stable if and only if the ROC the system function includes the unit circle. i.e r < 1. This is the condition for stability of the LSI system in terms of
z transform. Thus
For stable system |z| < 1
For unstable system |z| > 1
Marginally stable system |z| = 1
Poles inside unit circle gives stable system. Poles outside unit circle gives unstable system. Poles on unit circle give marginally stable system.
A causal and stable system must have a system function that converges for |z| > r < 1.
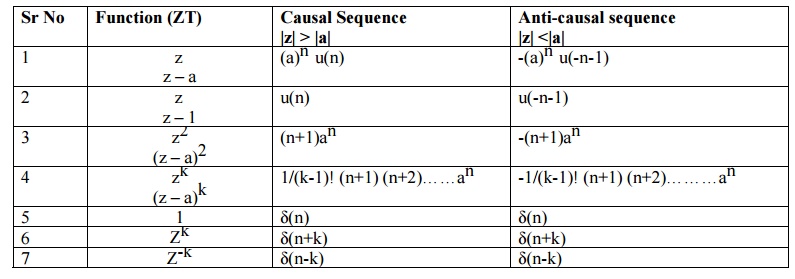
STANDARD INVERSE Z TRANSFORMS
ONE SIDED Z TRANSFORM


Properties of one sided z transform are same as that of two sided z transform except shifting property.
1) Time delay
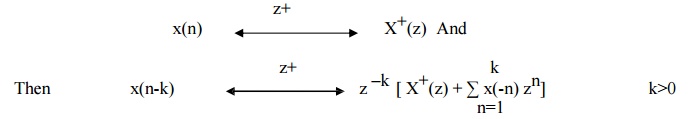
2) Time advance
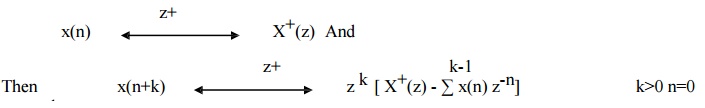
Examples:
Q) Determine one sided z transform for following signals
1) x(n)={1,2,3,4,5} 2) x(n)={1,2,3,4,5}
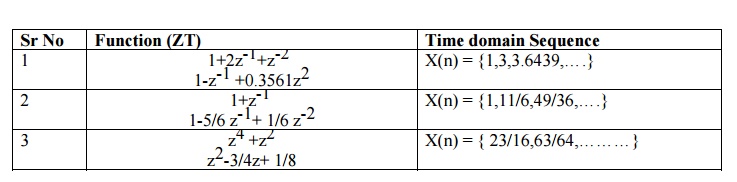
SOLUTION OF DIFFERENTIAL EQUATION
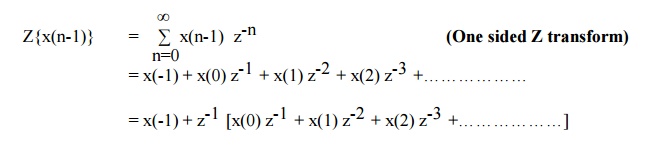
Z{ x(n-1) } = z-1 X(z) + x(-1)
Z{ x(n-2) } = z-2 X(z) + z-1 x(-1) + x(-2)
Similarly
Z{ x(n+1) } = z X(z) - z x(0)
Z{ x(n+2) } = z2 X(z) - z1 x(0) + x(1)
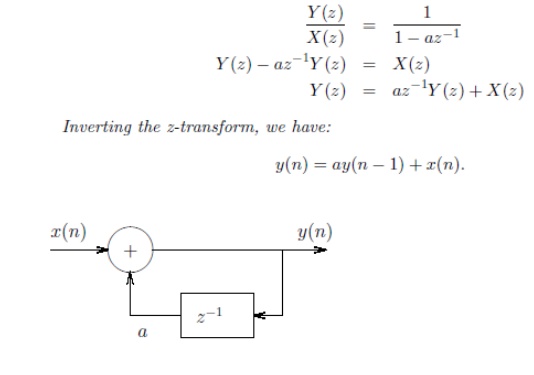
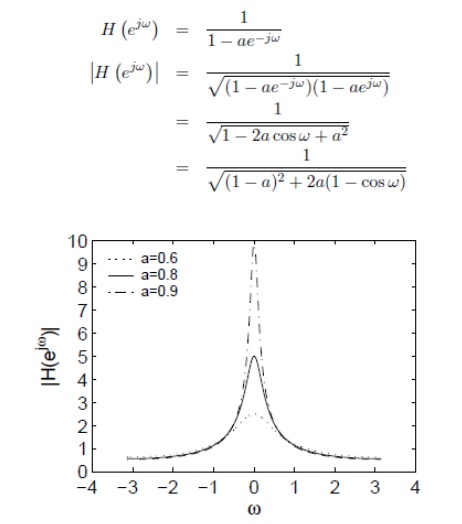
The transfer function H(ω) can be obtained from system function H(z) by putting z=ejω. Magnitude and phase response plot can be obtained by putting various values of ω.
First order Difference Equation
y(n) = x(n) + a y(n-1)
where y(n) = Output Response of the recursive system x(n) =
Input signal
a= Scaling factor
y(n-1) = Unit delay to output. Now
we will start at n=0
n=0 y(0) = x(0) + a y(-1) ….(1)
n=1 y(1) = x(1) + a y(0) ….(2)
= x(1) + a [ x(0) + a y(-1) ]
hence = a2 y(-1) + a x(0) + x(1) ….(3)
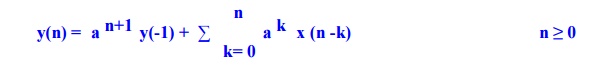
The first part (A) is response depending upon initial condition.
The second Part (B) is the response of the system to an input signal.
Zero state response (Forced response) : Consider initial condition are zero. (System is relaxed at time n=0) i.e y(-1) =0
Zero Input response (Natural response) : No input is forced as system is in non- relaxed initial condition. i.e y(-1) != 0
Total response is the sum of zero state response and zero input response.
Q) Determine zero input response for y(n) – 3y(n-1) – 4y(n-2)=0; (Initial Conditions are y(-1)=5 & y(-2)= 10) Answer: y(n)= 7 (-1)n + 48 (4)n
Q) A difference equation of the system is given below
Y(n)= 0.5 y(n-1) + x(n)
Determine a) System function
b) Pole zero plot
Unit sample response
A difference equation of the system is given below Y(n)= 0.7 y(n-1) – 0.12 y(n-2) + x(n-1) + x(n-2)
System Function b) Pole zero plot
Response of system to the input x(n) = nu(n)
Is the system stable? Comment on the result.
Q) A difference equation of the system is given below
Y(n)= 0.5 x(n) + 0.5 x(n-1)
Determine
a) System function
b) Pole zero plot
Unit sample response
Transfer function
Magnitude and phase plot
A difference equation of the system is given below a. Y(n)= 0.5 y(n-1) + x(n) + x(n-1)
Y(n)= x(n) + 3x(n-1) + 3x(n-2) + x(n-3)
System Function b) Pole zero plot
Unit sample response
Find values of y(n) for n=0,1,2,3,4,5 for x(n)= δ(n) for no initial condition.
Q) Solve second order difference equation
2x(n-2) – 3x(n-1) + x(n) = 3n-2 with x(-2)=-4/9 and x(-1)=-1/3.
Q) Solve second order difference equation x(n+2) + 3x(n+1) + 2x(n) with x(0)=0 and x(1)=1.
Related Topics