Important Short Questions and Answers: Signals and System

CLASSIFICATION OF SIGNALS AND SYSTEMS

1. Define Signal.

A signal is a function of one or more independent variables which contain some information. Eg: Radio signal, TV signal, Telephone signal etc.

2. Define System.

A system is a set of elements or functional block that are connected together and produces an output in response to an input signal.

Eg: An audio amplifier, attenuator, TV set etc.

3. Define CT signals.

Continuous time signals are defined for all values of time. It is also called as an analog signal and is represented by x(t).

Eg: AC waveform, ECG etc.

4. Define DT signal.

Discrete time signals are defined at discrete instances of time. It is represented by x(n). Eg: Amount deposited in a bank per month.

5. Give few examples for CT signals.

AC waveform, ECG,Temperature recorded over an interval of time etc.

6. Give few examples of DT signals.

Amount deposited in a bank per month,

7. Define unit step,ramp and delta functions for CT.

Unit step function is defined as

U(t) = 1 for t >= 0

0 otherwise

Unit ramp function is defined as

r(t) = t for t>=0

0 for t<0

Unit delta function is defined as

δ(t)= 1 for t=0

8. State the relation between step, ramp and delta functions (CT).

The relationship between unit step and unit delta function is

δ (t) = u(t)

The relationship between delta and unit ramp function is

δ (t).dt = r(t)

9. State the classification of CT signals.

The CT signals are classified as follows

·           Periodic and non periodic signals

·           Even and odd signals

·           Energy and power signals

·           Deterministic and random signals.

10. Define deterministic and random signals.

A deterministic signal is one which can be completely represented by mathematical equation at any time. In a deterministic signal there is no uncertainty with respect to its value at any time.

Eg: x(t)=coswt

x(n)=2wft

A random signal is one which cannot be represented by any mathematical equation. Eg: Noise generated in electronic components, transmission channels, cables etc.

11. Define Random signal.

There is no uncertainty about the deterministic signal. It is completely represented by mathematical expression.

 12. Define power and energy signals.

The signal x(t) is said to be power signal, if and only if the normalized average power p is finite and non-zero.

ie. 0<p<4

A signal x(t) is said to be energy signal if and only if the total normalized energy is finite and non-zero.

ie. 0<E< 4

13. Compare power and energy signals.

POWER SIGNAL

1. The normalized average power is finite and non-zero

2. Practical periodic signals are power signals

ENERGY SIGNALS

1. Total normalized energy is finite and non- zero.

2. Non-periodic signals are energy signals

14. Define odd and even signal.

A DT signal x(n) is said to be an even signal if x(-n)=x(n) and an odd signal if x(-n)=-x(n).

 A CT signal is x(t) is said to be an even signal if x(t)=x(-t) and an odd signal if x(-t)=-x(t).

15. Define periodic and aperiodic signals.

·        A signal is said to be periodic signal if it repeats at equal intervals.

·        Aperiodic signals do not repeat at regular intervals.

·        A CT signal which satisfies the equation x(t) = x(t+T0) is said to be periodic and a DT signal which satisfies the equation x(n) = x(n+N) is said to be periodic.

 16. State the classification or characteristics of CT and DT systems.

The DT and CT systems are according to their characteristics as follows

(i). Linear and Non-Linear systems

(ii). Time invariant and Time varying systems.

(iii). Causal and Non causal systems.

(iv). Stable and unstable systems.

(v). Static and dynamic systems.

(vi). Inverse systems.

17. Define linear and non-linear systems.

A system is said to be linear if superposition theorem applies to that system. If it does not satisfy the superposition theorem, then it is said to be a nonlinear system.

18. What are the properties linear system should satisfy?

A linear system should follow superposition principle. A linear system should satisfy,

f [ a₁ x₁(t) + a₂ x₂ (t)] = a ₁y₁(t) + a₂ y₂ (t)

where y₁(t) = f [ x₁(t) ]

y₂(t) = f[ x₂ (t) ]

19. What is the criterion for the system to possess BIBO stability?

A system is said to be BIBO stable if it produces bounded output for every bounded input.

20. Define shift invariance.

If the system produces same shift in the output as that of input, then it is called shift invariance or time invariance system. i.e.,

f [ x( t - t₁ ) ] = y ( t - t₁ )

21. Define Causal and non-Causal systems.

A system is said to be a causal if its output at anytime depends upon present and past inputs only. A system is said to be non-causal system if its output depends upon future inputs also.

22. Define time invariant and time varying systems.

A system is time invariant if the time shift in the input signal results in corresponding time shift in the output. A system which does not satisfy the above condition is time variant system.

23. Define stable and unstable systems.

When the system produces bounded output for bounded input, then the system is called bounded input, bounded output stable. A system which does not satisfy the above condition is called a unstable system.

24. Define Static and Dynamic system.

A system is said to be static or memory less if its output depends upon the present input only. The system is said to be dynamic with memory if its output depends upon the present and past input values.

25. Check causality of the system given by, y(n) = x(n-n_o)

If n_o ≥ 0, then output y(n) depends upon present or past input. Hence the system is causal. If n_o < 0 , the system become noncausal.

26. Check whether the given system is causal and stable.

y ( n ) = 3 x ( n - 2) + 3 x ( n + 2 )

Since y ( n ) depends upon x(n+2), this system is noncausal. As long as x (n – 2) and x ( n + 2 ) are bounded, the output y(n) will be bounded. Hence this system is stable.

27. When the discrete signal is said to be even?

A discrete time signal is said to be even when, x(-n) = x( n ).

For example cos(ωn) is an even signal.

28. Is diode a linear device? Give your reason.

Diode is nonlinear device since it operates only when forward biased. For negative bias, diode does not conduct.

29. Define power signal.

A signal is said to be power signal if its normalized power is nonzero and finite. i.e., 0 < P < ∞

30. Define signal. What are classifications of signals?

A function of one or more independent variables which contain some information is called signal.

31. What is the periodicity of x(t) = e^j100Πt + 30^o?

Here x(t) = e^j100Πt + 30^o

Comparing above equation with e^jωt+Ф, we get ω = 100 Π. Therefore period T is given as,

T=2 Π/ ω = 2 Π /100 Π = 1/50 = 0.02 sec.

32. Find the fundamental period of the signal x(n) = 3 e^j3Π(n+1/2)

X(n) = 3/5 e^{j 3Πn}. e^j3Π/2

= -j3/5 e^j3Πn

Here, ω=3Π, hence, f=3/2=k/N. Thus the fundamental period is N = 2.

33. Is the discrete time system describe by the equation y (n) = x(-n) causal or non causal ? Why?

Here y(n) = x(-n). If n = -2 then, y(-2 )= x(2)

Thus the output depends upon future inputs. Hence system is noncausal.

34. Is the system describe by the equation y(t) = x(2t) Time invariant or not? Why?

Output for delayed inputs becomes, y(t,t₁) =x(2t-t₁)

Delayed output will be, y(t-t₁) = x[2(t-t ₁)]

Since y(t,t1) ≠ y(t-t1) . The system is shift variant.

35. What is the period T of the signal x(t) = 2cos (n/4)?

Here, x (n) = 2cos (n/4) .

Compare x(n) with Acos (2∏ fn). This gives,

2∏fn = n/4 => F =1/8 ∏. Which is not rational.

Hence this is not periodic signal.

36. Is the system y(t) = y(t-1) + 2t y(t-2) time invariant ?

Here y(t-t1) = y(t-1-t1) + 2t y(t-2-t1) and

y(t t1) = y(t-t1-1) + 2(t- t1) y(t-t1-2).

Here y(t-t1) ≠ y(t t1). This is time variant system.

37. Check Whether the given system is causal and stable. y ( n ) = 3 x ( n - 2) + 3 x ( n + 2 )

Since y (n) depends upon x(n+2), this system is noncausal. As long as x (n – 2) and x(n + 2) are bounded, the output y(n) will be bounded. Hence this system is stable.

38. What is the periodicity of x(t) = e^j100Πt + 30^o ?

Here x(t) = e^j100Πt + 30^o

Comparing above equation with e^jωt+Ф , we get ω = 100 Π. Therefore period T is given as, T=2 Π/ ω = 2 Π /100 Π = 1/50 = 0.02 sec.

39. Find the fundamental period of the signal x(n)= 3 e^j3Π(n+1/2)

X(n) = 3/5 e^{j 3Πn}. e^j3Π/2

= -j3/5 e^j3Πn

Here, ω=3Π, hence, f=3/2=k/N. Thus the fundamental period is N = 2.

40. Define Sampling.

 Sampling is a process of converting a continuous time signal into discrete time Signal. After sampling the signal is defined at discrete instants of time and the time Interval between two subsequent sampling instants is called sampling interval.

41. What is an anti-aliasing filter?

A filter that is used to reject high frequency signals before it is sampled to reduce the aliasing is called anti-aliasing filter.

42. Define Sampling Theorem.

 It states that,

A band limited signal of finite energy, which has no frequency components higher than W hertz is completely described by specifying the value of the signal at instants of time separated by 1/2W seconds.

A band limited signal of finite energy which has no frequency components higher than W hertz is completely recovered from the knowledge of its samples taken at the rate of 2W samples per second, where W = 2f_m. These statements can be combinedly stated as

A bandlimited signal x(t) with X(j ω) = 0 for |ω| > ω_m is uniquely determined from its samples x(nT), if the sampling frequency f_s ≥ 2f_m, ie., sampling frequency must be atleast twice the highest frequency present in the signal.

43.Define Nyquist rate and Nyquist interval.

 Nyquist rate: When the sampling rate becomes exactly equal to 2W samples/sec, for a given bandwidth of fm or W Hertz, then it is called as Nyquist rate.

Nyquist rate = 2f_m samples/second

Nyquist interval: It is the time interval between any two adjacent samples when sampling rate is Nyquist rate.

Nyquist interval = 1/2W or 1/2f_m

44.Define aliasing.

When the high frequency interferes with low frequency and appears as low frequency, then the phenomenon is called aliasing.

45.What are the effects of aliasing?

The effects of aliasing are,

·           Since high and low frequencies interferes with each other distortion is generated

·           The data is lost and it cannot be recovered

 46.What is meant by a band limited signals?

A band limited signal is a signal x(t) for which the Fourier transform of x(t) is Zero above certain frequency ω_m.

x(t) < -- > X(j ω) = 0 for |ω| > ω_m = 2πf_m

47.What is the transfer function of a zero order hold?

The transfer function of a zero order hold is given by

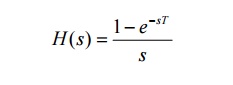
48.A signal x(t) whose spectrum is shown in figure is sampled at a rate of 300 samples/sec. What is the spectrum of the sampled discrete time signal.

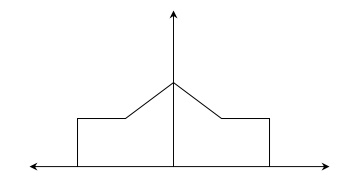
Solution:

f_m = 100 Hz

Nyquist rate = 2f_m = 200 Hz

Sampling frequency = f_s = 300 Hz

f_s > 2f_m , Therefore no aliasing takes place

The spectrum of the sampled signal repeats for every 300 Hz.

49. A signal having a spectrum ranging from near dc to 10 KHz is be sampled and Converted to discrete form. What is the minimum number of samples per second that must be take ensure recovery?

Solution:

Given: f_m = 10 KHz

From Nyquist rate the minimum no. of samples per second that must be taken to ensure recovery is,

f_s = 2f_m

= 2× 10 K = 20000samples/sec

50. A signal x(t) = sinc (150πt) is sampled at a rate of a) 100 Hz, b) 200 Hz, and c) 300Hz. For each of these cases, explain if you can recover the signal x(t) from the sampled signal.

Solution:

Given x(t) = sinc (150πt)

The spectrum of the signal x(t) is a rectangular pulse with a bandwidth (maximum frequency component) of 150π rad/sec as shown in figure.

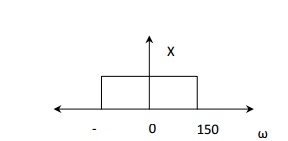
2πf_m = 150π

f_m = 75 Hz

Nyquist rate is 2f_m = 150 Hz

·           For the first case the sampling rate is 100Hz, which is less than Nyquist rate (under sampling). Therefore x(t) cannot be recovered from its samples.

·           And (c) in both cases the sampling rate is greater than Nyquist rate. Therefore x(t) can be recovered from its sample.

51. How can you minimize the aliasing error?

 Aliasing error can be reduced by choosing a sampling rate higher than Nyquist rate to avoid any spectral overlap. Prefiltering is done in order to ensure about the Nyquist frequency component so as to decide the appropriate sampling rate. By doing this we can reduce aliasing error.

52. Define z-transform and inverse z-transform.

The z-transform of a general discrete-time signal x(n) is defined as,

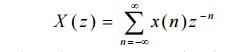
It is used to represent complex sinusoidal discrete time signal.

The inverse z-transform is given by,

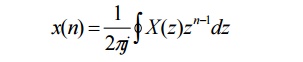
53. What do you mean by ROC? (or) Define Region of convergence.

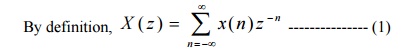
The z-transform exists when the infinite sum in equation (1) converges. A necessary condition for convergence is absolute summability of x(n)z^-n. The value of z for which the z-transform converges is called region of convergence.

54. What are left sided sequence and right sided sequence?

Left sided sequence is given by

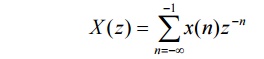
For this type of sequence the ROC is entire z-plane except at z = ∞.

Example: x(n) = {-3, -2, -1, 0}

Right sided sequence is given by

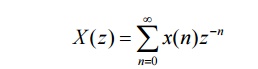
For this type of sequence the ROC is entire z-plane except z = 0.

Example: x(n) = { 1,0,3,-1,2}

55. Define two sided sequence (or) signal.

 A signal that has finite duration on both left and right sides is known as Two sided sequence.

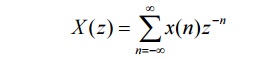
For such a type of sequences the ROC is entire z-plane except at z=0 and z=∞.

Example: x(n) = { 2,-1,3,2,1,0,2,3,-1}

56. List the properties of region of convergence for the z-transform.

·           The ROC of X(z) consists of a ring in the z-plane centered about the origin.

·           The ROC does not contain any poles.

·           If x(n) is of finite duration then the ROC is the entire z-plane except z = 0 and / or z = ∞.

·           If x(n) is a right sided sequence and if the circle |z| = r₀ is in the ROC then all finite values of z for which |z| > r₀ will also be in the ROC.

·           If x(n) is a left sided sequence and if the circle |z| = r₀ is in the ROC then all values of z for which 0< |z| < r₀ will also be in the ROC.

·           If x(n) is two sided sequence and if the circle |z| = r₀ is in the ROC then the ROC will consist of a ring in the z-plane that includes the circle |z| = r₀.

57. Determine the z-transform of the signal x(n) = αⁿ u(n) and also the ROC and pole & zero locations of X(z) in the z-plane.

Solution:

Given x(n) = αⁿ u(n)

58. List the properties of z-transform.

·           Linearity

·           Time shifting

·           Time reversal

·           Time scaling

·           Multiplication

·           Convolution

·           Parseval’s relation

59. What are the methods used to find inverse z-transform?

·           Long division method (or) Power series expansion

·           Residue method

·           Partial fraction method

·           Convolution method

60. State the Parseval’s theorem of z-transform.

If x1(n) and x2(n) are complex valued sequences, then the Parseval’s relation states that,

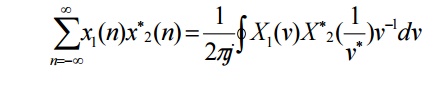
61.Determine the z-transform of unit step sequence.

The unit step sequence is given

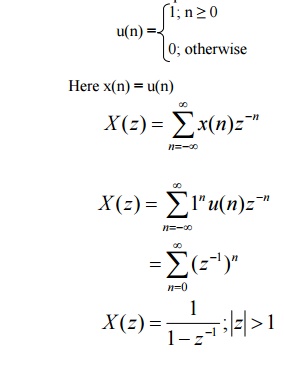
The ROC is at z > 1 ie., the area outside the unit circle

62. What is the relationship between the z-transform and FourierTransform?

The Fourier transform representation of a system is given by,

63.Determine the z-transform of the signal x(n) = -aⁿu(-n-1) & plot the ROC. Solution:

Given: x(n) = -aⁿu(-n-1)

By definition of z-transform,

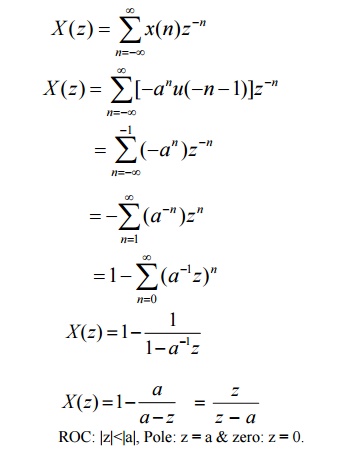
64. Find the left sided z-transform of the given sequence x[n]={2,4,-6,3,8,-2} Solution:

By definition of z-transform

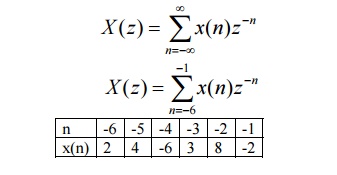
X(z) = x(-6)z⁶+x(-5)z⁵+x(-4)z⁴+x(-3)z³+x(-2)z²+x(-1)z

X(z) = 2z⁶+4z⁵+3z⁴+3z³+8z²+-2z

The ROC is entire z-plane except at z = ∞

65. How the stability of a system can be found in z-transform?

Let h(n) be a impulse response of a causal or non-causal LTI system and H(z) be the z-transform ofh(n). The stability of a system can be found from ROC using the theorem which states,

‘A Linear time system with the system function H(z) is BIBO stable if and only if the ROC for H(z) contains the unit circle.

66. What is the condition for causality in terms of z-transform?

 The condition for Linear time invariant system to be causal is given as,

h(n) = 0, n<0.

Where h(n) is the sample response of the system.

When the sequence is causal , its ROC is the exterior of the circle. i.e., |z|>r. LTI system is causal if and only if the ROC of the system function is exterior of the circle.

67. Find the system function and the impulse response of the system Described by the difference equation,

y(n) = x(n)+2x(n-1)-4x(n-2)+x(n-3) Solution:

The given difference equation is y(n) = x(n)+2x(n-1)-4x(n-2)+x(n-3) Taking z-transform,

Y(z) = X(z)+2z^-1X(z) – 4z^-2X(z)+z^-3X(z)

The system function, H (z) = 1+ 2z ⁻¹ − 4z ⁻² + z ⁻³

The impulse response is h(n) = {1,2,-4,1}

   68. Consider an LTI system with difference equation,

   y(n)- 3/4 y(n-1)+1/8 y(n-2) = 2x(n). Find H(z).

   Solution:

   Given, y(n)-3/4 y(n-1)+1/8 y(n-2) = 2x(n) Taking z-transform,

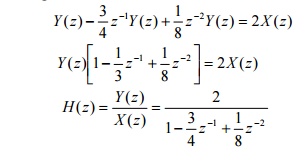
    69. State and prove the time shifting property of z-transform.

   The time shifting property of z-transform states that

   if X(z) = z{x(n)}then x(n-k) ↔ z^-k X(z)

   where k is an integer.

   Proof:

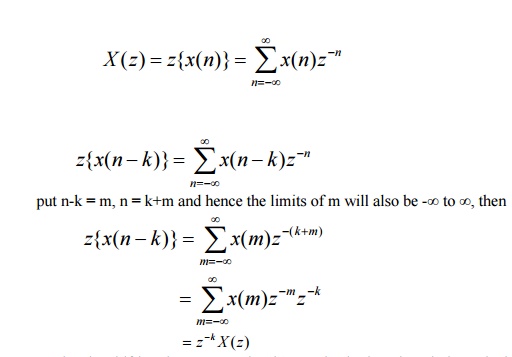
   Thus by shifting the sequence by ’k’ samples in time domain is equivalent to multiplying its z-transform by z^-k.

   70.State initial value theorem of z-transform.

   If x(n) is a causal sequence then its initial value is given by

   71. Determine the system function of the discrete system described by difference equation y(n)-1/2 y(n-1)+1/4 y(n-2) = x(n)-x(n-1).

   Solution:

   y(n)-1/2 y(n-1)+1/4 y(n-2) = x(n)-x(n-1) Taking z-transform,

   Y(z) -1/2z^-1Y(z) + 1/4z^-2Y(z) = X(z)-z^-1X(z)

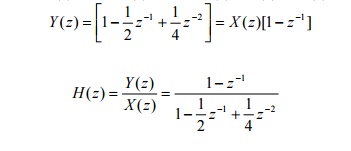
   72. What is the transfer function of a system whose poles are at -0.3±j0.4 and a zero at -0.2?

   Poles are at z = -0.3±j0.4

   ∴ Denominator polynomial = [z-(-0.3+j0.4)][z-(-0.3-j0.4)] Zero at z = -0.2

   ∴ Numerator polynomial = z+0.2 The transfer function is given by,

   73. Define one-sided and two-sided z-transform. (Nov/Dec 2004)

   One sided z-transform is defined as,

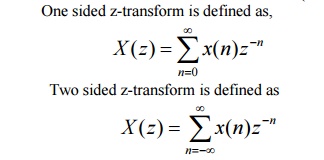
   74. State any two properties of autocorrelation function.

                                                             i.      A fundamental property of the autocorrelation is symmetry, R(i)=R(-i), which is  easy to prove from the definition.

                                                           ii.      The autocorrelation of a periodic function is, itself, periodic with the same period.

   75. State convolution property.

   Convolution property states that if x₁ (n)← ^z→ X₁ (z) and

   x₂ (n)← ^z→ X ₂ (z)

   Then x₁ (n) ∗ x₂ (n)← ^z→ X₁ (z)X ₂ (z)

GLOSSARY:

1. Signal.

A signal is a function of one or more independent variables which contain some information. Eg: Radio signal, TV signal, Telephone signal etc.

2. System.

A system is a set of elements or functional block that are connected together and produces an output in response to an input signal.

Eg: An audio amplifier, attenuator, TV set etc.

3. Continuous Time signals.

Continuous time signals are defined for all values of time. It is also called as an analog signal and is represented by x(t).

Eg: AC waveform, ECG etc.

4. Discrete Time signals.

Discrete time signals are defined at discrete instances of time. It is represented by x(n). Eg: Amount deposited in a bank per month.

5. Sampling.

Sampling is a process of converting a continuous time signal into discrete time Signal. After sampling the signal is defined at discrete instants of time and the time Interval between two subsequent sampling instants is called sampling interval.

6.Anti-aliasing filter.

A filter that is used to reject high frequency signals before it is sampled to reduce the aliasing is called anti-aliasing filter.

7. Nyquist rate: When the sampling rate becomes exactly equal to 2W samples/sec, for a given bandwidth of fm or W Hertz, then it is called as Nyquist rate.

Nyquist rate = 2f_m samples/second.

8. Z-transform and Inverse z-transform.

The z-transform of a general discrete-time signal x(n) is defined as,

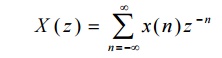
It is used to represent complex sinusoidal discrete time signal.

The inverse z-transform is given by,

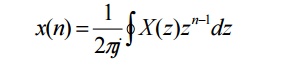
9. Region of convergence.

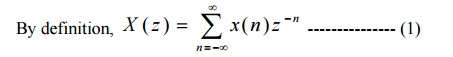
The z-transform exists when the infinite sum in equation (1) converges. A necessary condition for convergence is absolute summability of x(n)z^-n. The value of z for which the z-transform converges is called region of convergence.

10. Left sided sequence and Right sided sequence

Left sided sequence is given by

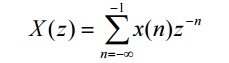
For this type of sequence the ROC is entire z-plane except at z = ∞.

Right sided sequence is given by

For this type of sequence the ROC is entire z-plane except z = 0.

11. Parseval’s theorem of z-transform.

If x1(n) and x2(n) are complex valued sequences, then the Parseval’s relation states that,

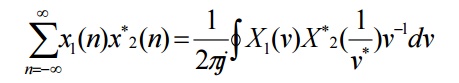
12. LTI System.

A System is said to be linear and Time Invariant if it Satisfies the Superposition Principle and if the input is delayed than the output also delayed by the same amount.