Basic Block Diagram of A/D Converter

BASIC BLOCK DIAGRAM OF A/D CONVERTER

SAMPLING THEOREM

It is the process of converting continuous time signal into a discrete time signal by taking samples of the continuous time signal at discrete time instants.

X[n]= Xa(t) where t= nTs = n/Fs      ….(1)

When sampling at a rate of fs samples/sec, if k is any positive or negative integer, we cannot distinguish between the samples values of fa Hz and a sine wave of (fa+ kfs) Hz. Thus (fa + kfs) wave is alias or image of a wave.

Thus Sampling Theorem states that if the highest frequency in an analog signal is Fmax and the signal is sampled at the rate fs > 2Fmax then x(t) can be exactly recovered from its sample values. This sampling rate is called Nyquist rate of sampling. The imaging or aliasing starts after Fs/2 hence folding frequency is fs/2. If the frequency is less than or equal to 1/2 it will be represented properly.

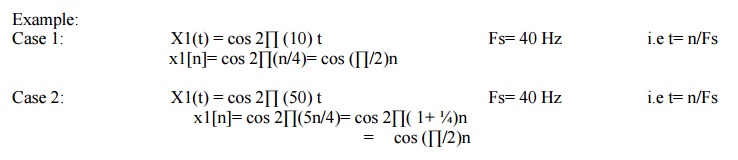
Thus the frequency 50 Hz, 90 Hz , 130 Hz … are alias of the frequency 10 Hz at the sampling rate of 40 samples/sec

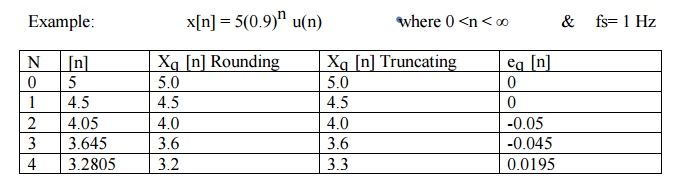
QUANTIZATION

The process of converting a discrete time continuous amplitude signal into a digital signal by expressing each sample value as a finite number of digits is called quantization. The error introduced in representing the continuous values signal by a finite set of discrete value levels is called quantization error or quantization noise.

Quantization Step/Resolution : The difference between the two quantization levels is called quantization step. It is given by ∆ = XMax – xMin / L-1 where L indicates Number of quantization levels.

CODING/ENCODING

Each quantization level is assigned a unique binary code. In the encoding operation, the quantization sample value is converted to the binary equivalent of that quantization level.

If 16 quantization levels are present, 4 bits are required. Thus bits required in the coder is the smallest integer greater than or equal to Log2 L. i.e b= Log2 L Thus Sampling frequency is calculated as fs=Bit rate / b.

ANTI-ALIASING FILTER

When processing the analog signal using DSP system, it is sampled at some rate depending upon the bandwidth. For example if speech signal is to be processed the frequencies upon 3khz can be used. Hence the sampling rate of 6khz can be used. But the speech signal also contains some frequency components more than 3khz. Hence a sampling rate of 6khz will introduce aliasing. Hence signal should be band limited to avoid aliasing.

The signal can be band limited by passing it through a filter (LPF) which blocks or attenuates all the frequency components outside the specific bandwidth. Hence called as Anti aliasing filter or pre-filter. (Block Diagram)

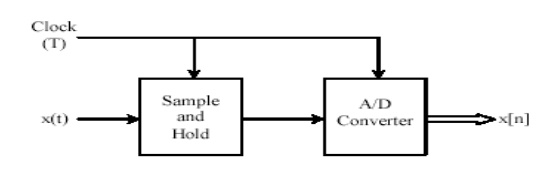
SAMPLE-AND-HOLD CIRCUIT:

The sampling of an analogue continuous-time signal is normally implemented using a device called an analogue-to- digital converter (A/D). The continuous-time signal is first passed through a device called a sample-and-hold (S/H) whose function is to measure the input signal value at the clock instant and hold it fixed for a time interval long enough for the A/D operation to complete. Analogue-to-digital conversion is potentially a slow operation, and a variation of the input voltage during the conversion may disrupt the operation of the converter. The S/H prevents such disruption by keeping the input voltage constant during the conversion. This is schematically illustrated by Figure.

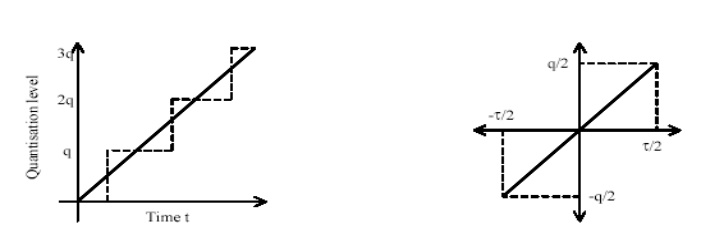
After a continuous-time signal has been through the A/D converter, the quantized output may differ from the input value. The maximum possible output value after the quantization process could be up to half the quantization level q above or q below the ideal output value. This deviation from the ideal output value is called the quantization error. In order to reduce this effect, we increases the number of bits.

Q) Calculate Nyquist Rate for the analog signal x(t)

1) x(t)= 4 cos 50 ∏t + 8 sin 300∏t –cos 100∏t                               Fn=300 Hz

2) x(t)= 2 cos 2000∏t+ 3 sin 6000∏t + 8 cos 12000∏t                   Fn=12KHz

3) x(t)= 4 cos 100∏t                                                                         Fn=100 Hz

Q) The following four analog sinusoidal are sampled with the fs=40Hz. Find out corresponding time signals and comment on them

X1(t)= cos 2∏(10)t

X2(t)= cos 2∏(50)t

X3(t)= cos 2∏(90)t

X4(t)= cos 2∏(130)t

Q) Signal x1(t)=10cos2∏(1000)t+ 5 cos2∏(5000)t. Determine Nyquist rate. If the signal is sampled at 4khz will the signal be recovered from its samples.

Q) Signal x1(t)=3 cos 600∏t+ 2cos800∏t. The link is operated at 10000 bits/sec and each input sample is quantized into 1024 different levels. Determine Nyquist rate, sampling frequency, folding frequency & resolution.

DIFFERENCE BETWEEN FIR AND IIR

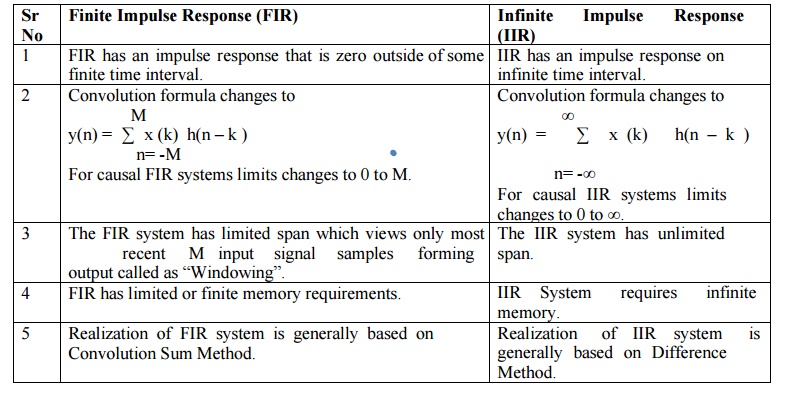
Discrete time systems has one more type of classification.

a)        Recursive Systems

b)       Non-Recursive Systems