Correlation: Types, Properties

CORRELATION:

It is frequently necessary to establish similarity between one set of data and another. It means we would like to correlate two processes or data. Correlation is closely related to convolution, because the correlation is essentially convolution of two data sequences in which one of the sequences has been reversed.

Applications are in

1.   Images processing for robotic vision or remote sensing by satellite in which data from different image is compared

2.   In radar and sonar systems for range and position finding in which transmitted and reflected waveforms are compared.

3.   Correlation is also used in detection and identifying of signals in noise.

4.   Computation of average power in waveforms.

5.   Identification of binary codeword in pulse code modulation system.

DIFFERENCE BETWEEN LINEAR CONVOLUTION AND CORRELATION

Linear Convolution

1. In case of convolution two signal sequences input signal and impulse response given by the same system is calculated

2. Our main aim is to calculate the response given by the system.

3. Linear Convolution is given by the equation y(n) = x(n) * h(n) & calculated as

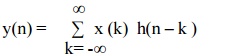
4. Linear convolution is commutative

Correlation

1. In case of Correlation, two signal sequences are just compared.

2. Our main aim is to measure the degree to which two signals are similar and thus to extract some information that depends to a large extent on the application

3. Received signal sequence is given as Y(n) = α x(n-D) + ω(n) Where α= Attenuation Factor D= Delay ω(n) = Noise signal

4. Not commutative.

TYPES OF CORRELATION

Under Correlation there are two classes.

1) CROSS CORRELATION: When the correlation of two different sequences x(n) and y(n) is performed it is called as Cross correlation. Cross-correlation of x(n) and y(n) is rxy(l) which can be mathematically expressed as

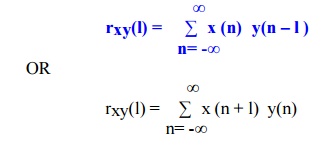
2) AUTO CORRELATION: In Auto-correlation we correlate signal x(n) with itself, which can be mathematically expressed as

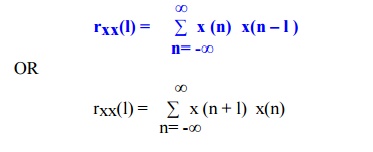
PROPERTIES OF CORRELATION

1) The cross-correlation is not commutative.

 rxy(l) = ryx(-l)

2) The cross-correlation is equivalent to convolution of one sequence with folded version of another sequence.

rxy(l) = x(l) * y(-l).

3) The autocorrelation sequence is an even function. rxx(l) = rxx(-l)

Examples:

Q) Determine cross-correlation sequence

x(n)={2, -1, 3, 7,1,2, -3} & y(n)={1, -1, 2, -2, 4, 1, -2 ,5}

Answer:      rxy(l) = {10, -9, 19, 36, -14, 33, 0,7, 13, -18, 16, -7, 5, -3}

Q) Determine autocorrelation sequence     

x(n)={1, 2, 1, 1}   Answer:      rxx(l) = {1, 3, 5, 7, 5, 3, 1}